1 引言
近几年,为了解决全球能源危机和环境污染日益严重的问题,越来越多的可再生能源并入到电网中,同时对于接口变换器的要求也越来越高。其中级联H桥逆变器由于具有多电平的优势,能够使交流侧输出电压更接近正弦波,减小了滤波电感的体积,因此在储能并网逆变器中得到广泛应用[1 ⇓ -3 ] 并得到了国内外学者的广泛研究[4 ⇓ ⇓ ⇓ -8 ] 。
随着越来越多的新能源接入电网,电网电压中处于不平衡以及含有谐波等非理想状态是不可避免的,当电网电压处于非理想状态时,受到电网电压负序和谐波分量的影响,传统控制策略下的并网逆变器输出电流将会发生畸变,低次谐波含量高以及产生输出功率波动等问题,使逆变器和电网的运行情况恶化。为了解决电网电压处于非理想状态时传统控制策略下的并网逆变器所出现的问题,文献[9 ⇓ ⇓ ⇓ -13 ]提出的控制策略在dq 坐标系下采用比例积分(Proportional integral,PI)控制器和αβ 坐标系下采用比例谐振(Proportional resonance,PR)控制器来对并网电流进行控制。但是,当电网电压不可避免地会发生畸变导致电网电压中含有低次谐波分量时,采用比例积分控制方法会导致并网电流含有相应的谐波分量,进而导致并网电流含有较大的低次谐波分量;采用比例谐振控制方法虽然能够有效地抑制并网电流中的低次谐波分量,但是当电网处 于不平衡时会导致输出电流不平衡。文献[14 -15 ]提出基于双序前馈解耦的重复控制和比例积分控制器相结合的控制方法,在电网电压处于非理想状态时,虽然在一定程度上相比于单独的PI控制器能够减小并网电流的谐波含量,但是当电网电压中含有低次谐波分量时,该方法并不能有效地降低由此引起的并网电流中的低次谐波含量,文献[16 ]提出利用比例积分谐振控制器来消除由网侧电压畸变引起的单相变流器交流电流中的低次谐波,但是该文献中对于参数整定的过程较为模糊且无法得出控制器参数具体的选择范围,没有明确的约束规则,使得系统无法工作在较为理想的状态。文献[17 ⇓ -19 ]提出一种有限集模型预测控制,实现电网不平衡下并网控制,该方法不需要复杂的调制策略,但是为了满足并网要求,需要较大的总谐波失真(Total harmonic distortion,THD),因此会增加系统成本。文献[20 ]针对低次谐波抑制问题,提出基于自适应陷波器的谐波抑制方法。通过在主电流环中加入基于自适应陷波器的谐波抑制策略,可同时抑制多次谐波电流,具有控制结构简单的优点,取得了较好的效果。但其采用的自适应算法较复杂,其中步长参数选择会对算法收敛性影响较大从而影响谐波补偿效果。
通过上述分析,当电网电压处于非理想状态时,采用上述的控制策略,会使得系统出现并网电流性能下降,无法消除系统中的某些特定次低次谐波以及THD较大等问题,同时上述控制策略中也并未给出明确的参数设计依据。本文针对以上控制策略的不足,提出采用准比例积分谐振控制器来对系统的并网电流进行控制,并指出在控制器参数设计过程中需要满足的相位裕度、幅值裕度、基频增益约束等约束条件,并为了使系统能够保持稳定以及拥有较大的带宽,给出了满足条件的参数范围内的具体参数数值。最后通过仿真加以验证,仿真结果表明,上述所提出的控制策略既能快速有效地跟踪并网电流又能有效地抑制并网电流中的低次谐波,也可以有效提高并网电流的电能质量。
2 级联储能变流器拓扑结构及数学模型
2.1 级联储能变流器拓扑结构
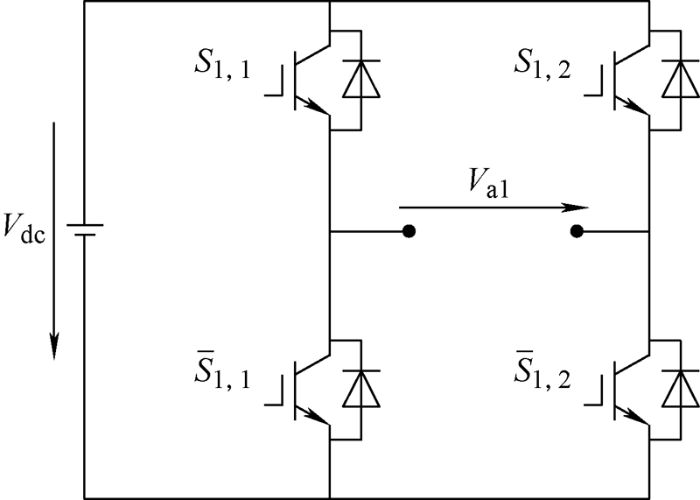
级联H桥储能变流器每个单元都是有独立直流电源的单相全桥逆变器,电路拓扑结构如图1 所示,这种拓扑能够把隔离的多个直流电压叠加得到交流侧中高压输出,直接接入中高压电网。本文主要研究了一种基于级联H桥拓扑结构直接接入10 kV电网的储能变流器的设计方案,并对其控制策略展开研究。
图1
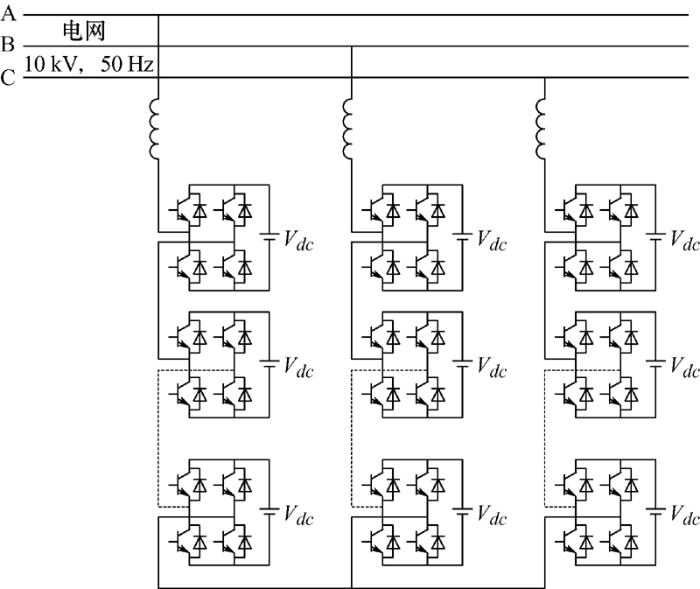
级联储能变流器的每一相由多个H桥单元串联而成,三相结构采用星形连接方式,经滤波电抗接入10 kV电网。级联储能变流器的具体电路拓扑结构如图2 所示。
图2
级联H桥储能变流器在接入6.3 kV电网时的级联单元个数通常为8个,在接入10 kV电网时通常为12个,因此本文取级联单元个数N =12。
2.2 级联储能变流器数学模型
图2 给出了中压直挂式级联储能变流器系统的主电路结构,整个系统为三相星形联结,经过滤波电抗接入中压电网,每一相由N 个单元模块级联而成,其中每一个H桥单元模块的电路如图1 所示,在采用移相载波调制时,同一桥臂上、下开关管的开关状态互补,由此可得H桥单元在不同开关状态下,其直流侧电压和交流侧输出电压的关系如表1 所示。
在级联型储能变流器中,其输出电压由N 个单元模块的输出电压叠加得到,则总输出电压如式(1)所示
(1) ${{V}_{k}}={{V}_{dc}}\sum\limits_{i=0}^{N}{({{S}_{i,1}}-{{S}_{i,2}})\ \ \ \ k=a,b,c}$
式中,Si ,1 和Si ,2 是第i 个单元的二进制开关 信号。
由基尔霍夫电压定律可得级联型储能变流器的网侧电压电流时域模型如式(2)所示
(2) $\left\{ \begin{align} & {{V}_{k}}-{{V}_{sk}}-(R{{i}_{k}}+L\frac{d{{i}_{k}}}{dt})={{V}_{{o}'o}}\ \ \ \ k=a,b,c \\ & {{V}_{{o}'o}}=\frac{1}{3}({{V}_{a}}+{{V}_{b}}+{{V}_{c}}-{{V}_{sa}}-{{V}_{sb}}-{{V}_{sc}}) \\ \end{align} \right.$
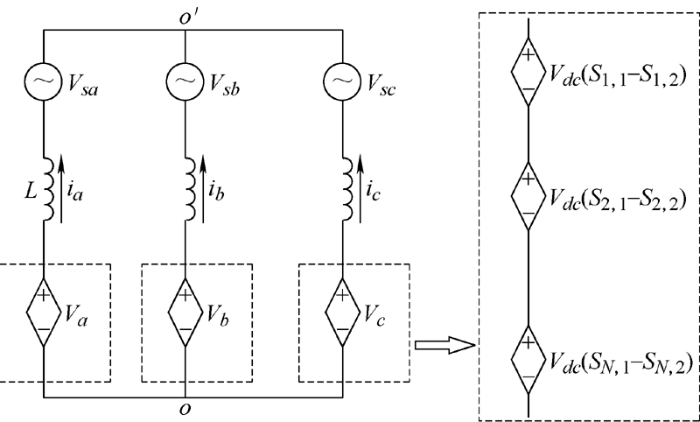
其中网侧电流方向如图3 所示,Vsk 为电网k 相电压,Vk 为每相的桥臂输出电压,Vo'o 为系统的零序电压分量,由储能变流器的输出电压和电网电压来确定。
图3
由上述分析可得级联储能变流器的等效电路如图3 所示。
3 控制策略与参数设计分析
3.1 同步旋转坐标系下双电流闭环控制策略
当非理想电网情况出现时,若仍采用理想电网下的控制结构,网侧电流中的负序分量将会无法得到控制,从而引起逆变器交流侧过电流,电流谐波增大的情况,这些问题轻则影响并网逆变器的正常运行,重则烧毁器件[21 ] ,为了解决这一问题,需要对网侧电流中的正序、负序分量分别进行控制。
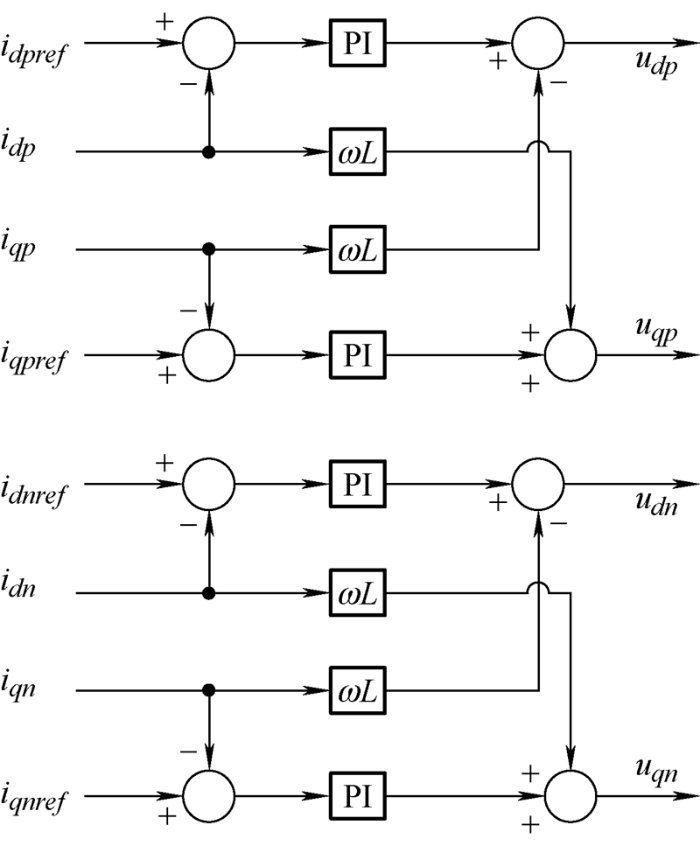
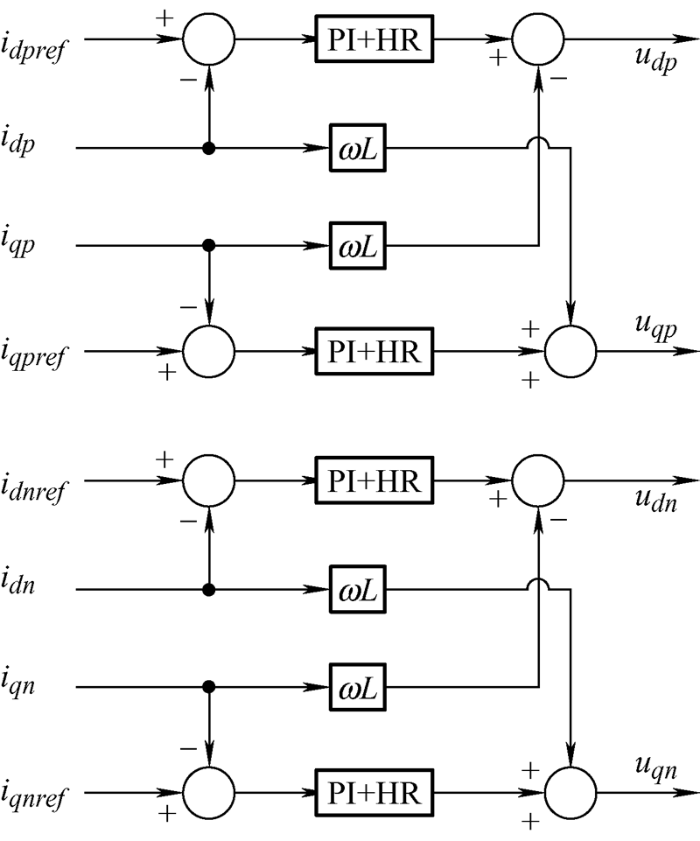
dq 同步旋转坐标系下的逆变器数学模型存在d 、q 轴相互耦合的情况,这使得控制系统变得复杂,无法实现d 、q 轴分量的单独控制,因此需要进行解耦控制。为了实现解耦控制,需要在控制量中加入与其大小相等、方向相反的量与耦合量相抵消。由以上分析可得dq 旋转同步坐标系下的网侧电流控制方程如式(3)所示。
(3) $\left\{ \begin{align} & {{u}_{dp}}={{k}_{p}}(1+\frac{1}{{{T}_{i}}s})({{i}_{dpref}}-{{i}_{dp}})-\omega L{{i}_{qp}} \\ & {{u}_{qp}}={{k}_{p}}(1+\frac{1}{{{T}_{i}}s})({{i}_{qpref}}-{{i}_{qp}})+\omega L{{i}_{dp}} \\ & {{u}_{dn}}={{k}_{p}}(1+\frac{1}{{{T}_{i}}s})({{i}_{dnref}}-{{i}_{dn}})+\omega L{{i}_{qn}} \\ & {{u}_{qn}}={{k}_{p}}(1+\frac{1}{{{T}_{i}}s})({{i}_{qnref}}-{{i}_{qn}})-\omega L{{i}_{dn}} \\ \end{align} \right.$
式中,kp 、Ti 分别为PI控制器的比例增益与积分时间常数,udp 、uqp 、udn 、uqn 分别表示调制波电压信号的正负序dq 轴分量,idpref 、iqpref 、idnref 与iqnref 分别表示网侧电流的给定正负序dq 轴分量,idp 、iqp 、idn 与iqn 分别表示网侧电流的正负序dq 轴分量。由式(3)可以看出经过控制器输出与前馈解耦控制进而得到输出的调制波信号。最终的网侧电流控制框图如图4 所示。
图4
根据交流侧数学模型及网侧电流控制方程,在经过dq 轴解耦处理后,以d 轴为例电流环的控制结构图如图5 所示。
图5
在交流电网中含有-5次、+7次谐波的情况下,经过dq 变换后会产生6次谐波,若采用上述的传统电流环d 、q 轴PI控制算法,是不能对6次谐波电流进行无静差跟踪的,虽然可以通过增加比例系数Kp 和积分系数Ki 的值使得PI控制器的增益有所提高,但Kp 和Ki 过大,有可能导致系统不稳定或临界稳定,所以PI控制器跟踪交流量必定存在稳态误差,这样交流电流中的-5次、+7谐波就无法消除。
因此,本文提出了一种既能对d 、q 轴直流有功分量进行无静差跟踪,又能有效抑制低次电流谐波的PI-HR控制器。通过对三相级联H桥储能逆变器侧的电流和网侧电压的采样值进行Park变换,对级联H桥储能变流器的网侧电压进行正负序分离以及对网侧电流在dq 轴下进行解耦和正负序分离,采用同步旋转坐标系下双电流闭环控制策略来实现对并网电流的跟踪,其控制结构图如图6 所示。利用准比例积分谐振控制器来抑制网侧电流的波动和低次谐波分量,能够实现对中压直挂型级联储能变流器并网电流的良好控制,可适应多种功率应用场合,提高了级联储能变流器的入网电能品质,同时能够有效地抑制网侧电流中的低次谐波分量。本文也从多个系统稳定性约束条件出发,构建了比较系统完整的控制器参数设计方法。
图6
根据交流侧数学模型可知,系统在d 轴和q 轴下参数相互独立并且对称,因此以d 轴为例,可得到采用本文提出的控制策略电流环控制结构图如 图7 所示。
图7
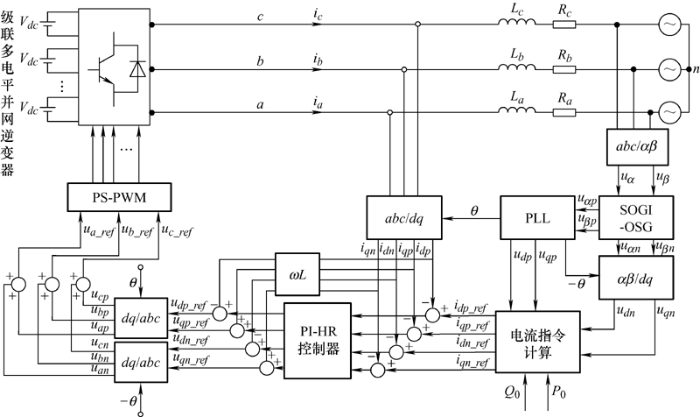
综上所述,本文在非理想电网下基于准比例积分谐振控制器的级联储能变流器系统整体结构示意框图如图8 所示。
图8
图8
非理想电网下基于准比例积分谐振控制器的级联储能变流器整体结构示意图
3.2 准比例积分谐振控制器的参数设计
按照首先设计PI控制器参数,然后根据系统带宽设计HR控制器参数的设计步骤对控制器参数进行设计。为了简化分析过程,暂不考虑电网电压的扰动,则由图7 所示的电流环结构框图,可得系统的开环传递函数为
(4) ${{G}_{op}}=\frac{{{i}_{d}}_{(s)}}{i_{d(s)}^{*}}={{G}_{c(s)}}{{G}_{d(s)}}{{K}_{PWM}}\frac{1}{sL+R}$
式中,Gc ( s ) 为PI+HR的传递函数,具体表达式为
(5) ${{G}_{c(s)}}={{K}_{p}}+\frac{{{K}_{i}}}{s}+\sum\limits_{h=0}^{n}{{{K}_{rh}}\frac{2{{\omega }_{ih}}s}{{{s}^{2}}+2{{\omega }_{ih}}s+\omega _{h}^{2}}}$
式中,Gd ( s ) 为采样、计算等效的延时环节,具体表达式为
(6) ${{G}_{d(s)}}=\frac{1}{{{T}_{s}}}\exp \left( -s{{T}_{s}} \right)\frac{1-\exp \left( -s{{T}_{s}} \right)}{s}\approx \exp \left( -1.5s{{T}_{s}} \right)$
并网逆变器系统在截止频率ωc 处,系统开环传递函数的幅值增益大小|Gop (s =jωc )|=1,此时的PI控制器的传递函数可等效为Gc (s )≈Kp ,则由此可推导出电流控制器参数Kp 的表达式为
(7) ${{K}_{p}}=\frac{\sqrt{{{({{\omega }_{c}}L)}^{2}}+{{R}^{2}}}}{{{K}_{PWM}}}$
(8) PI参数设计需要满足相位裕度和幅值裕度的约束条件。首先在系统的穿越频率ωh 处PI控制器的传递函数可近似为Gc ( s ) ≈Kp ,考虑到开环传递函数在穿越频率处的相位为-π,即∠Gop (s=jωh )= -π,ωh 需要满足式
(8) $\tan (1.5{{\omega }_{h}}{{T}_{s}})+\frac{{{\omega }_{h}}L}{R}=0$
(9) $GM=-20\lg \left| {{G}_{op}}(s=j{{\omega }_{h}}) \right|$
(10) ${{K}_{p\_GM}}={{10}^{-\frac{GM}{20}}}\cdot \frac{\sqrt{{{({{\omega }_{h}}L)}^{2}}+{{R}^{2}}}}{{{K}_{PWM}}}$
系统的幅值裕度约束为GM ≥GM 0 ,可得GM 0 对Kp 的约束为
(11) ${{K}_{p}}\le {{K}_{p\_G{{M}_{0}}}}({{K}_{p}},{{\omega }_{h}})$
(12) ${{K}_{p\_G{{M}_{0}}}}={{10}^{-\frac{G{{M}_{0}}}{20}}}\cdot \frac{\sqrt{{{({{\omega }_{h}}L)}^{2}}+{{R}^{2}}}}{{{K}_{PWM}}}$
联立式(8)和式(12)即可得出幅值裕度约束GM 0 对Kp 的具体约束范围。在系统截止频率ωc 处,相位裕度PM 为
(13) $\begin{align} & PM={{180}^{{}^\circ }}+\angle {{G}_{op}}(s=j{{\omega }_{c}})={{180}^{{}^\circ }}- \\ & \text{ }\arctan \frac{{{K}_{i}}}{{{\omega }_{c}}{{K}_{p}}}-1.5{{\omega }_{c}}{{T}_{s}}-\arctan \frac{{{\omega }_{c}}L}{R} \\ \end{align}$
(14) $\begin{matrix} {{K}_{i\_PM}}= \\ \frac{{{K}_{p}}{{\omega }_{c}}[{{\omega }_{c}}L+R\tan (PM+1.5{{\omega }_{c}}{{T}_{s}})]}{{{\omega }_{c}}L\tan (PM+1.5{{\omega }_{c}}{{T}_{s}})-R} \\ \end{matrix}$
系统的相位裕度约束为PM ≥PM 0 ,可得PM 0 对Ki 的约束为
(15) ${{K}_{i}}\le {{K}_{i\_P{{M}_{0}}}}({{K}_{p}},{{\omega }_{c}})$
(16) $\begin{matrix} {{K}_{i\_P{{M}_{0}}}}({{K}_{p}},{{\omega }_{c}})= \\ \frac{{{K}_{p}}{{\omega }_{c}}[{{\omega }_{c}}L+R\tan (P{{M}_{0}}+1.5{{\omega }_{c}}{{T}_{s}})]}{{{\omega }_{c}}L\tan (P{{M}_{0}}+1.5{{\omega }_{c}}{{T}_{s}})-R} \\ \end{matrix}$
最后,因需要保证在基频f 0 处开环传递函数有足够大的增益,可得下述约束。
(17) $\begin{align} & {{T}_{{{f}_{0}}}}=20\lg \left| {{G}_{op}}(j{{\omega }_{0}}) \right|= \\ & 20\lg \left| \frac{{{K}_{PWM}}({{K}_{p}}+\frac{{{K}_{i}}}{j{{\omega }_{0}}})}{j{{\omega }_{0}}L+R} \right| \\ \end{align}$
系统的基频增益约束为Tf 0 ≥Tf 0 ' T f 0 ' Ki 的约束为
(18) ${{K}_{i}}\ge {{K}_{i\_{{T}_{f{0}'}}}}({{K}_{p}})$
(19) $\begin{matrix} {{K}_{i\_{{T}_{f{0}'}}}}= \\ \sqrt{{{\left( \frac{{{10}^{\frac{{{T}_{{{f}_{0}}^{\prime }}}}{20}}}}{{{K}_{PWM}}} \right)}^{2}}\times [{{({{\omega }_{0}}L)}^{2}}+{{R}^{2}}]-K_{P}^{2}}\times {{\omega }_{0}} \\ \end{matrix}$
综上,联立式(7)、式(10)、式(14)和式(19)可得PI控制器参数Kp 、Ki 的取值范围为
(20) $\left\{ \begin{align} & {{K}_{p}}\le {{K}_{p\_G{{M}_{0}}}} \\ & {{K}_{i\_{{T}_{{{f}_{0}}^{\prime }}}}}({{K}_{p}})\le {{K}_{i}}\le {{K}_{i\_P{{M}_{0}}}}({{K}_{p}}) \\ \end{align} \right.$
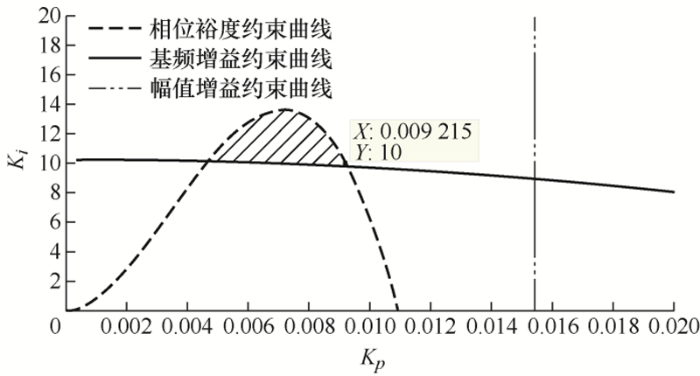
由上述分析,为了保持控制系统的稳定性能,系统在ωc 处的相位裕度应维持在40°~70°,在ωh 处的幅值裕度应大于等于3 dB,基频增益应取得足够大,根据以上条件,以相位裕度45°,幅值裕度3 dB,基频增益40 dB为临界条件,采样频率取20 kHz,滤波器参数L 为12 mH,R 为0.02 Ω时,可绘制出如图9 所示的约束曲线。由图9 可知,为了使系统保持稳定,Kp 、Ki 的取值范围应同时满足相位裕度约束条件、幅值裕度约束条件和基频增益约束条件,则根据式(20)的约束方程可得控制器参数Kp 、Ki 的可选区域为如图9 所示的阴影部分。
图9
在控制器参数满足基本要求的前提下,为提高对低次谐波的抑制能力,本文选取尽可能大的截止频率ω c ,即在参数的可取范围内选择Kp 的最大值。此时Kp 的取值满足
(21) ${{K}_{i\_{{T}_{{{f}_{0}}^{\prime }}}}}({{K}_{p}})={{K}_{i\_P{{M}_{0}}}}({{K}_{p}})$
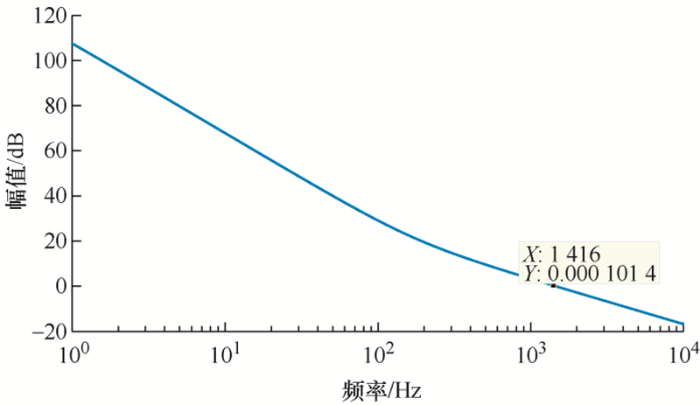
在确定好Kp 、Ki 后,可绘制其开环传递函数的伯德图如图10 所示。
图10
由图10 可知,此时系统的截止频率fc 为1 416 Hz,根据文献[22 -23 ]中的经验公式可知Kr 的取值可由式(22)得到
(22) ${{K}_{r}}=\frac{{{\omega }_{c}}\cdot {{K}_{p}}}{20\cdot \pi }=1.3$
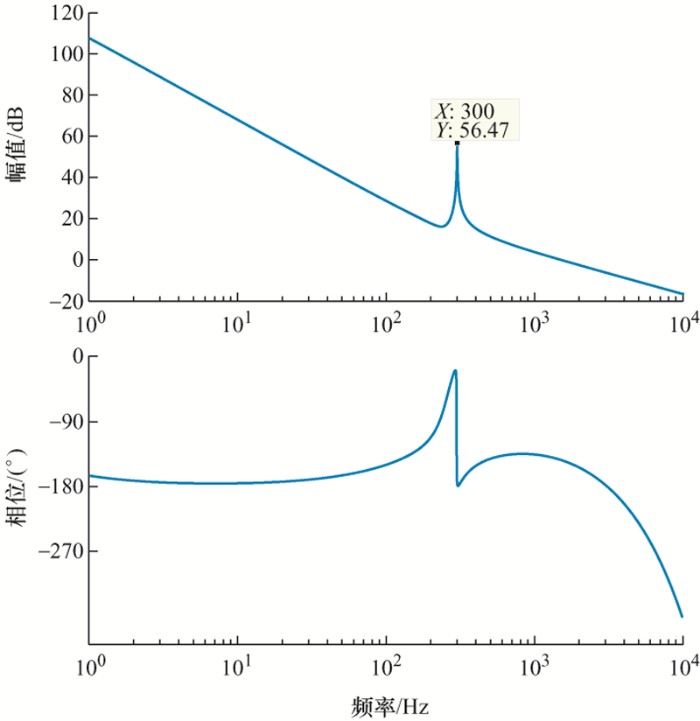
则由上述分析得到的Kp 、Ki 、Kr ,可绘制系统在PI-HR控制器下的开环传递函数伯德图如图11 所示。
由图11 可知系统的开环传递函数在频率为300 Hz处有较大的开环增益,由此可得到其闭环传递函数在此频率处的增益接近于1,即能够有效地跟踪给定参考电流。因此当给定参考电流不含有此频率的谐波分量时,其能够有效地抑制并网电流中所存在的+7次谐波以及 -5次谐波含量。又由图11 可知在谐波点附近一定带宽的频率范围内,其开环传递函数仍能维持较高的开环增益,解决了实际谐波频率与设计谐波频率略有偏差时,增益大幅下降的问题。由上述分析可知本文设计控制器方法的可行性与正确性。
图11
4 仿真分析
为了验证本文所提控制策略的有效性和准确性,在Matlab/Simulink平台上搭建了基于非理想电网下中压直挂型级联H桥多电平三相逆变器的控制系统模型,用直流电压源模拟储能组件,仿真参数如表2 所示。
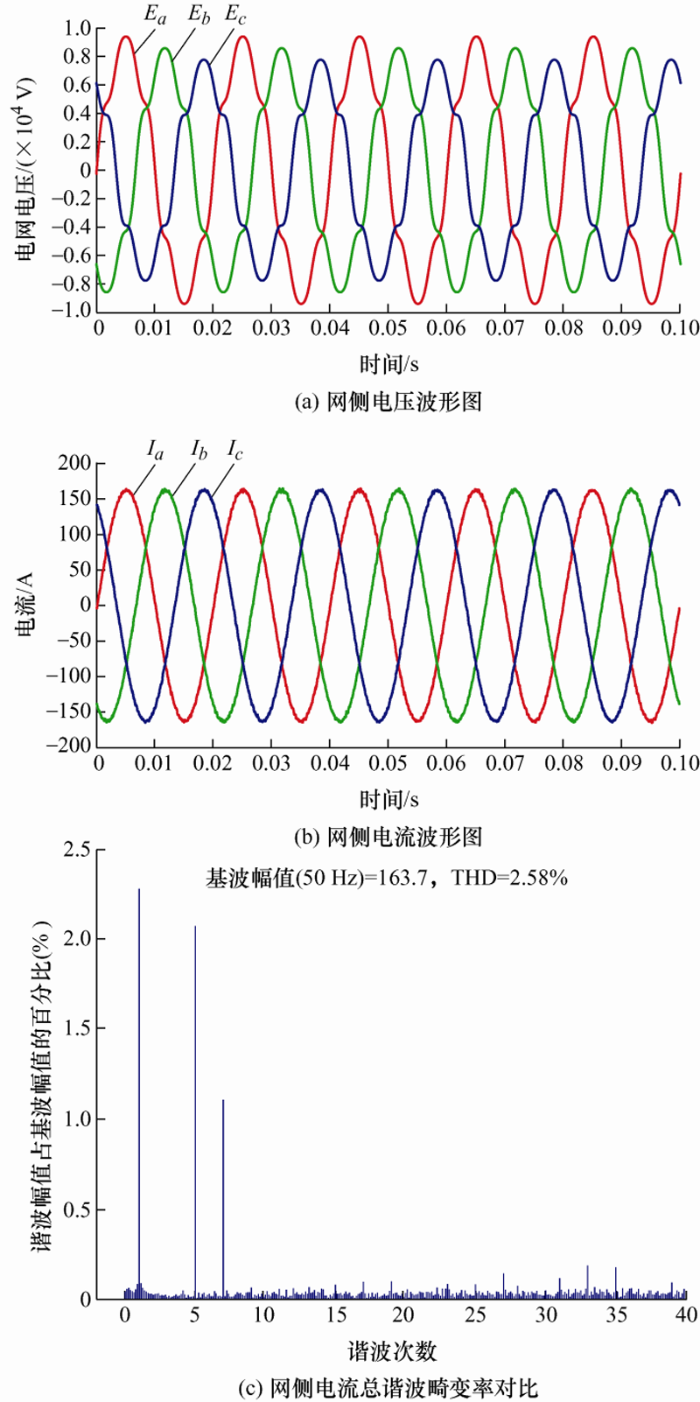
为了说明在非理想电网条件下,本文所提出的控制方法以及本文提出的对于控制器参数设计方法的有效性与优势。对比仿真分析了文献[7 ]和文献[13 ]提出的采用比例积分控制器和比例谐振控制器来提高级联H桥输出电流质量的方法,其中图12 和图13 为电网电压在非理想状态时分别采用PI和PR控制器以及采用文献中的控制器参数设计方法所得到的仿真波形图,其中电网电压非理想状态主要体现在a相电压上升为原来的1.1倍,c相电压跌落为原来的0.9倍,同时三相电网电压中分别出现表2 中的谐波电压。
图12
图13
图12 为电网电压在非理想状态时采用PI控制器的仿真波形图,由图12 可以看出在电网电压处于上述非理想状态时采用PI控制器,虽然网侧电流在到达稳态时能够得到比较理想的波形,但是网侧电流中含有较高的由电网电压引起的5次与7次谐波分量。
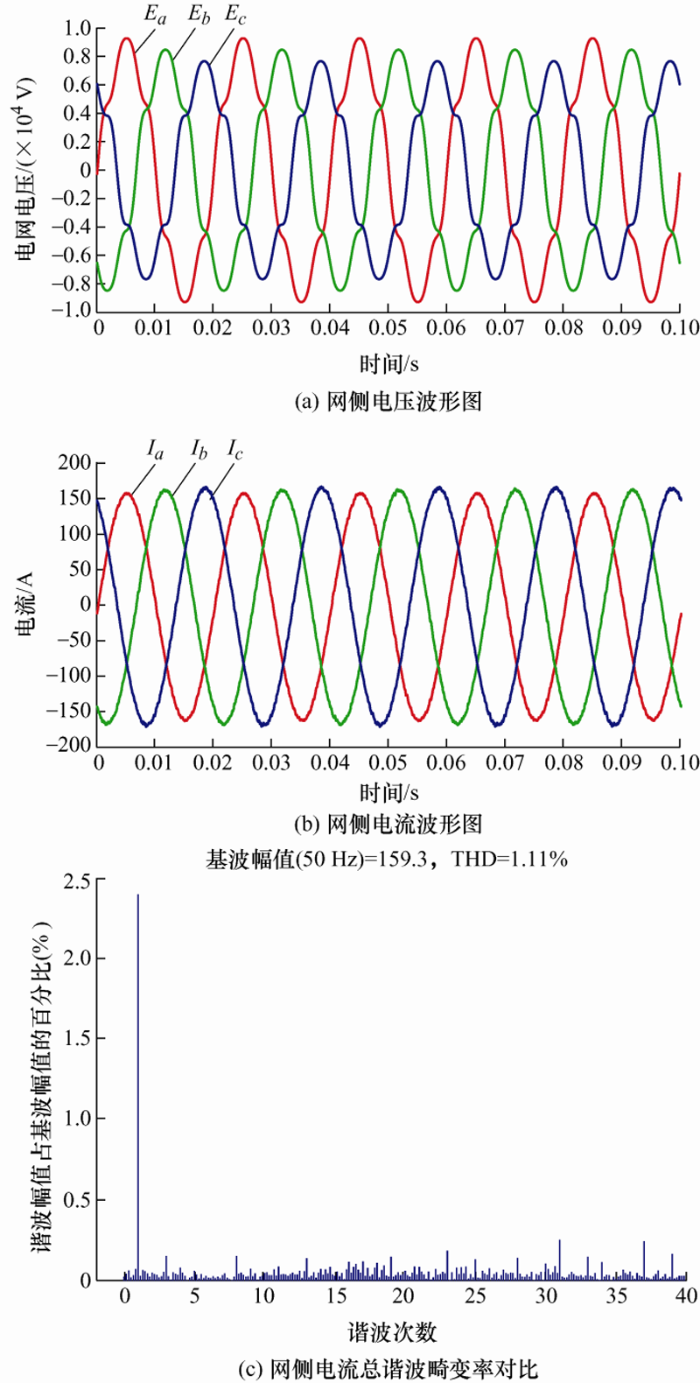
图13 为电网电压在非理想状态时采用PR控制器以及采用其中的参数设计方法所得到的仿真波形图。由图13 可以看出在采用PR控制器时,当电网电压处于谐波污染时,能够有效地抑制由电网电压引起的网侧电流中含有的5次与7次谐波分量,也能有效地降低电流的THD。但是当电网在含有谐波污染的同时又处于不平衡状态时,其电流波形虽然未发生畸变,但是却呈现出了三相电流不平衡的状态,需要进一步地改善输出电流的波形质量。
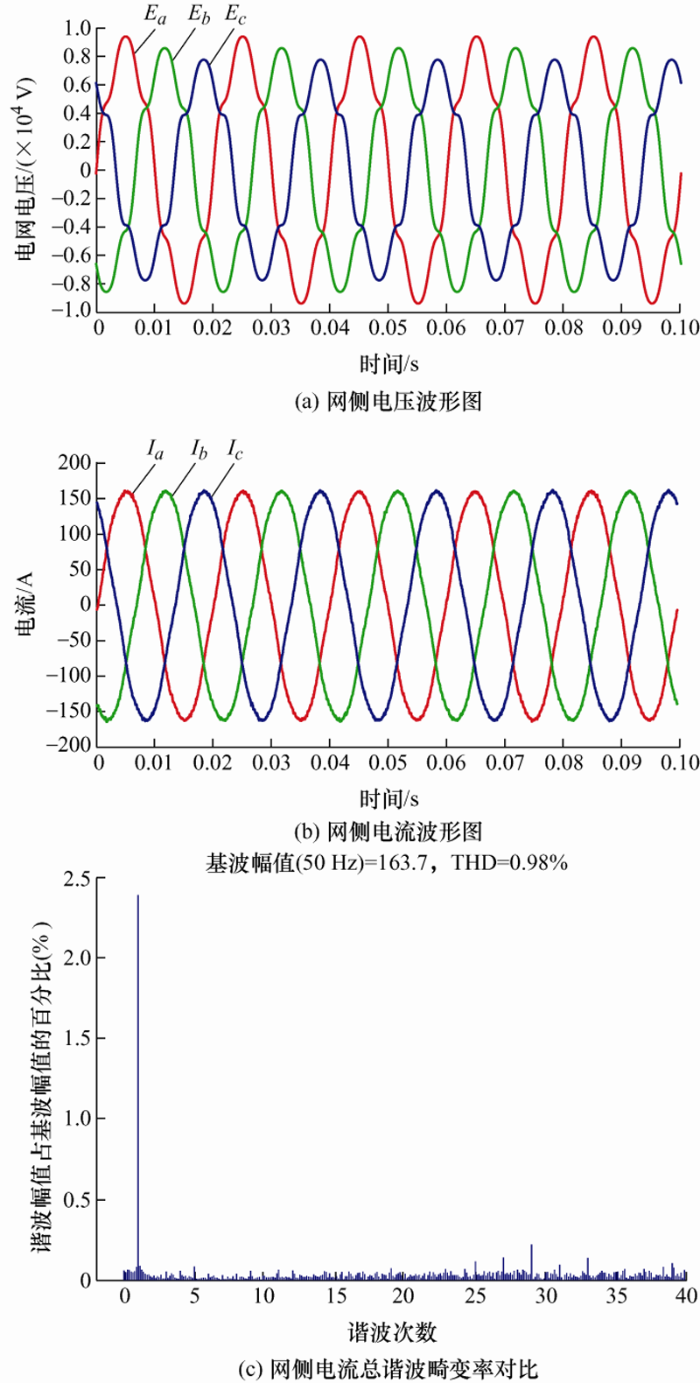
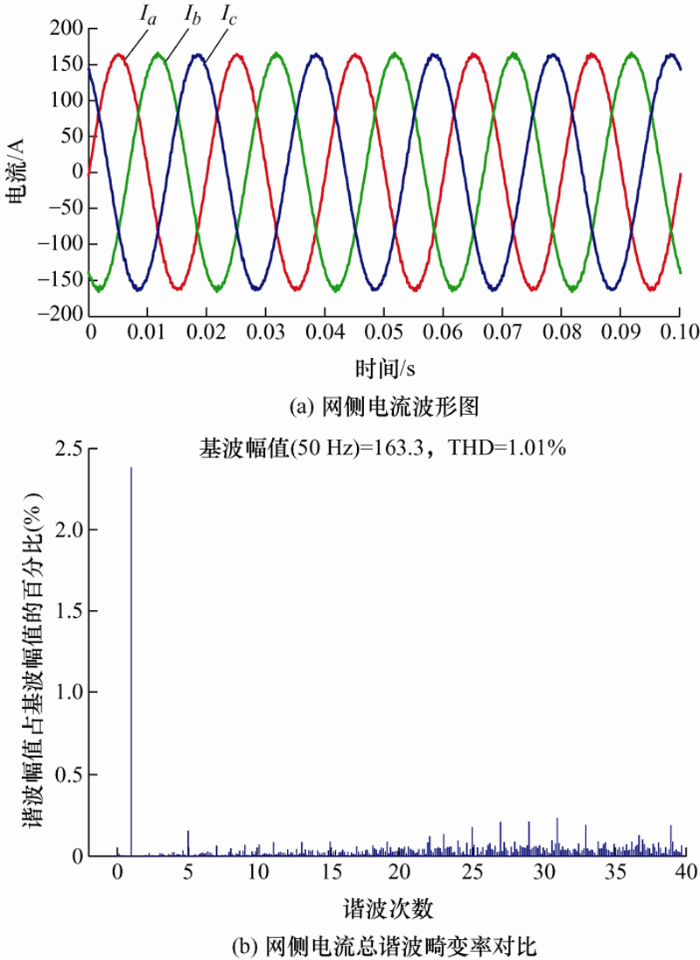
通过对上述对比仿真的分析,针对以上控制方法的不足之处,本文提出了基于准比例积分谐振调节器的同步旋转坐标系下双电流闭环控制策略以及所对应的系统完整的控制器参数设计方法。图14 为本文所提出的控制方法仿真波形图。由图14 可以看出,所提方法不仅可以有效地抑制由电网电压引起的网侧电流中含有的5次与7次谐波分量,使网侧电流的THD降低到0.98%,还能使网侧电流的波形更接近于正弦化,进一步地改善了并网电流质量。
图14
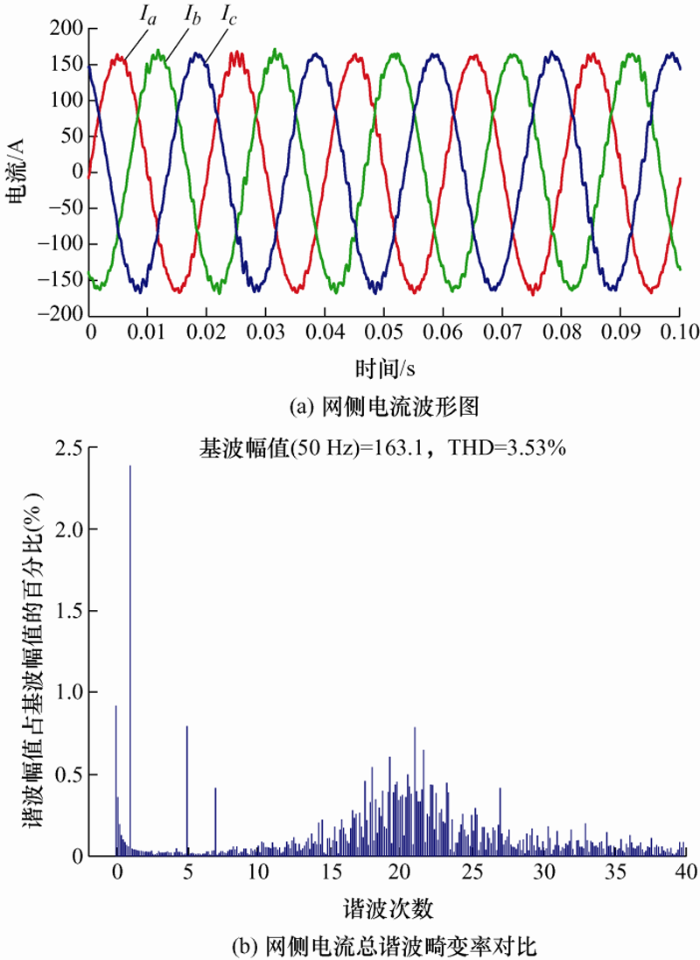
为了进一步验证所提控制器参数设计的适用 性和优势,通过分别选取参数设计方法范围以内 和范围以外两组参数进行仿真对比,如图15 和图16 所示。通过对比可以看出,当选择的参数在所提控制器参数设计方法范围内时,网侧电流的THD为1.01%,其中5次、7次谐波含量明显降低,且总网侧电流的THD由3.53%下降到1.01%。由此可以看出本文所提控制器参数设计方法的有效性和优势。
图15
图16
5 结论
针对当电网电压不平衡且电网存在谐波污染时引起的中压直挂式级联H桥储能变流器并网电流性能下降以及存在低次谐波含量高的问题,本文提出一种非理想电网条件下基于dq 轴下采用准比例积分谐振(PI-HR)控制器来对级联储能变流器入网电流进行改善的控制策略,建立了同步旋转坐标系下双电流闭环控制策略的分析模型,并通过具体分析阐述了控制器参数的设计过程,最后通过Matlab/ Simulink进行仿真验证,得到以下结论。
(1) 通过对同步旋转坐标系下双电流闭环控制策略的分析,当电网中含有-5次、+7次谐波的情况下,经过dq 变换后会产生6次谐波,传统的控制方法无法实现对于特定次低次谐波的消除。本文所提出的基于准比例积分谐振控制器采用同步旋转坐标系下双电流闭环控制策略能够有效地实现对并网电流的跟踪,明显地降低并网电流中的低次谐波含量。
(2) 在对准比例积分谐振控制器的参数设计分析中,指出在参数设计的过程中需要满足相位裕度、幅值裕度、基频增益约束等约束条件,联合建立了对控制器参数的约束方程,构建了比较系统完整的控制器参数设计方法。通过对控制系统的开环传递函数伯德图进行分析,同时分别选取本文所设计的控制器参数范围内以及范围外的两组参数进行对比仿真,验证了本文所提出控制方法的适用性以及优势。
(3) 通过仿真对比分析,和仅采用PI控制器与PR控制器相比,本文所提出的控制策略不仅能够在电网电压处于非理想状态时有效地降低并网电流的低次谐波含量,还能很好地改善并网电流的波形质量以及进一步地降低并网电流的THD。
参考文献
View Option
[1]
龚秋英 , 马鑫金 , 李艳 . 一种级联型多电平并网逆变器控制策略的研究
[J]. 电气传动 , 2020 , 50 (11 ):13 -16 .
[本文引用: 1]
GONG Qiuying MA Xinjin LI Yan Research on a cascaded multilevel grid-connected inverter control strategy
[J]. Electric Drive , 2020 , 50 (11 ):13 -16 .
[本文引用: 1]
[2]
YU Y KONSTANTINOU G HREDZAK B et al. Power balance optimization of cascaded H-bridge multilevel converters for large-scale photovoltaic integration
[J]. IEEE Transactions on Power Electronics , 2016 , 31 (2 ):1108 -1120 .
DOI:10.1109/TPEL.2015.2407884
URL
[本文引用: 1]
[3]
RODRIGUEZ J LAI J S FANG Zhengpeng Multilevel inverters:A survey of topologies,controls,and applications
[J]. IEEE Transactions on Industrial Electronics , 2007 , 49 (4 ):724 -738 .
DOI:10.1109/TIE.2002.801052
URL
[本文引用: 1]
[4]
DAHER S SCHMID J ANTUNES F L M Multilevel inverter topologies for stand-alone PV systems
[J]. IEEE Transactions on Industrial Electronics , 2008 , 55 (7 ):2703 -2712 .
DOI:10.1109/TIE.2008.922601
URL
[本文引用: 1]
[5]
MALINOWSKI M GOPAKUMAR K RODRIGUEZ J et al. A survey on cascaded multilevel inverters
[J]. IEEE Transactions on Industrial Electronics , 2010 , 57 (7 ):2197 -2206 .
DOI:10.1109/TIE.2009.2030767
URL
[本文引用: 1]
[6]
毛苏闽 , 蔡旭 . 大容量链式电池储能功率调节系统控制策略
[J]. 电网技术 , 2012 , 36 (9 ):226 -231 .
[本文引用: 1]
MAO Sumin CAI Xu Large-capacity chain battery energy storage power regulation system control strategy
[J]. Power System Technology , 2012 , 36 (9 ):226 -231 .
[本文引用: 1]
[7]
蔡旭 , 李睿 , 刘畅 , 等 . 高压直挂储能功率变换技术与世界首例应用
[J]. 中国电机工程学报 , 2020 , 40 (1 ):200 -211 ,387.
[本文引用: 2]
CAI Xu LI Rui LIU Chang et al. High-voltage direct-mounted energy storage power conversion technology and the world’s first application
[J]. Proceedings of the Chinese Society for Electrical Engineering , 2020 , 40 (1 ):200 -211 ,387.
[本文引用: 2]
[8]
LI Y WANG Y LI B Q Generalized theory of phase-shifted carrier pwm for cascaded H-bridge converters and modular multilevel converters
[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics , 2016 , 4 (2 ):589 -605 .
DOI:10.1109/JESTPE.2015.2476699
URL
[本文引用: 1]
[9]
刘力 , 于佳丽 . 不对称电网电压下光伏并网逆变器控制策略研究
[J]. 太阳能学报 , 2017 , 38 (10 ):2848 -2856 .
[本文引用: 1]
LIU Li YU Jiali Research on control strategy of photovoltaic grid-connected inverter under asymmetric grid voltage
[J]. Acta Solar Energy , 2017 , 38 (10 ):2848 -2856 .
[本文引用: 1]
[10]
MIRHOSSEINI M POU J AGELIDIS V G et al. A three-phase frequency-adaptive phase-locked loop for independent single-phase operation
[J]. IEEE Transactions on Power Electronics , 2014 , 29 (12 ):6255 -6259 .
DOI:10.1109/TPEL.2014.2328657
URL
[本文引用: 1]
[11]
陈红生 , 杨苹 , 曾晓生 . 单相并网逆变器准比例谐振控制器的设计
[J]. 低压电器 , 2012 (22 ):19 -23 ,59.
[本文引用: 1]
CHEN Hongsheng YANG Ping ZENG Xiaosheng Design of quasi-proportional resonant controller for single-phase grid-connected inverter
[J]. Low Voltage Electrical Apparatus , 2012 (22 ):19 -23 ,59.
[本文引用: 1]
[12]
TRINH Q LEE H An enhanced grid current compensator for grid-connected distributed generation under nonlinear loads and grid voltage distortions
[J]. IEEE Transactions on Industrial Electronics , 2014 , 61 (12 ):6528 -6537 .
DOI:10.1109/TIE.2014.2320218
URL
[本文引用: 1]
[13]
许运华 , 王清 , 孟红秀 . 电网畸变级联H桥逆变器控制研究
[J]. 电气传动 , 2019 , 49 (10 ):44 -47 .
[本文引用: 2]
XU Yunhua WANG Qing MENG Hongxiu Research on the control of power grid distortion cascaded H-bridge inverter
[J]. Electric Drive , 2019 , 49 (10 ):44 -47 .
[本文引用: 2]
[14]
杨浩 , 宋国杰 , 滕馥遥 , 等 . 基于双序前馈解耦的光伏逆变器并网控制策略
[J]. 太阳能学报 , 2021 , 42 (1 ):77 -84 .
[本文引用: 1]
YANG Hao SONG Guojie TENG Fuyao et al. Grid-connected photovoltaic inverter control strategy based on double-sequence feedforward decoupling
[J]. Acta Solar Energy , 2021 , 42 (1 ):77 -84 .
[本文引用: 1]
[15]
JIANG W MA W WANG J et al. Deadbeat control based on current predictive calibration for grid-connected converter under unbalanced grid voltage
[J]. IEEE Transactions on Industrial Electronics , 2017 , 64 (7 ):5479 -5491 .
DOI:10.1109/TIE.2017.2674620
URL
[本文引用: 1]
[16]
张馨予 , 张钢 , 钱江林 , 等 . 具有低次谐波抑制能力的PIR控制器设计
[J]. 电工技术学报 , 2016 , 31 (S2 ):19 -27 .
[本文引用: 1]
ZHANG Xinyu ZHANG Gang QIAN Jianglin et al. Design of PIR controller with low-order harmonic suppression ability
[J]. Transactions of China Electrotechnical Society , 2016 , 31 (S2 ):19 -27 .
[本文引用: 1]
[17]
AGUILERA R P ACUNA P YU Yifan et al. Predictive control of cascaded H-bridge converters under unbalanced power generation
[J]. IEEE Transactions on Industrial Electronics , 2017 , 64 (1 ):4 -13 .
DOI:10.1109/TIE.2016.2605618
URL
[本文引用: 1]
[18]
李大海 , 陈素 . 多电平级联H桥逆变器的模型预测控制策略
[J]. 电力电容器与无功补偿 , 2021 , 42 (1 ):159 -165 .
[本文引用: 1]
LI Dahai CHEN Su Model predictive control strategy for multi-level cascaded H-bridge inverters
[J]. Power Capacitors and Reactive Power Compensation , 2021 , 42 (1 ):159 -165 .
[本文引用: 1]
[19]
金涛 , 沈学宇 , 苏泰新 , 等 . 不平衡电网下并网逆变器的模型预测电流限幅灵活控制
[J]. 电工技术学报 , 2019 , 34 (11 ):2342 -2353 .
[本文引用: 1]
JIN Tao SHEN Xueyu SU Taixin et al. Model-predicted current limiting flexible control of grid-connected inverters in unbalanced grids
[J]. Transactions of China Electrotechnical Society , 2019 , 34 (11 ):2342 -2353 .
[本文引用: 1]
[20]
代攀 . 永磁同步电机电流环谐波抑制技术研究 [D]. 武汉 : 华中科技大学 , 2014 .
[本文引用: 1]
DAI Pan Research on current loop harmonic suppression technology of permanent magnet synchronous motor [D]. Wuhan : Huazhong University of Science and Technology , 2014 .
[本文引用: 1]
[21]
姜卫东 , 吴志清 , 佘阳阳 , 等 . 电网不平衡时抑制有功功率二次波动的并网逆变器控制策略
[J]. 电力系统自动化 , 2014 , 38 (15 ):106 -111 .
[本文引用: 1]
JIANG Weidong WU Zhiqing SHE Yangyang et al. Grid-connected inverter control strategy for restraining the secondary fluctuation of active power when the grid is unbalanced
[J]. Automation of Electric Power Systems , 2014 , 38 (15 ):106 -111 .
[本文引用: 1]
[22]
HOLMES D G LIPO T A MCGRATH B P et al. Optimized design of stationary frame three phase AC current regulators
[J]. IEEE Trans. Power Electron. , 2009 , 24 (11 ):2417 -2426 .
DOI:10.1109/TPEL.2009.2029548
URL
[本文引用: 1]
[23]
QIANG Q XIE S HUANG L et al. Harmonic suppression and stability enhancement for parallel multiple grid-connected inverters based on passive inverter output impedance
[J]. IEEE Trans. Power Electron. , 2017 , 64 (9 ):7587 -7598 .
[本文引用: 1]
一种级联型多电平并网逆变器控制策略的研究
1
2020
... 近几年,为了解决全球能源危机和环境污染日益严重的问题,越来越多的可再生能源并入到电网中,同时对于接口变换器的要求也越来越高.其中级联H桥逆变器由于具有多电平的优势,能够使交流侧输出电压更接近正弦波,减小了滤波电感的体积,因此在储能并网逆变器中得到广泛应用[1 ⇓ -3 ] 并得到了国内外学者的广泛研究[4 ⇓ ⇓ ⇓ -8 ] . ...
Research on a cascaded multilevel grid-connected inverter control strategy
1
2020
... 近几年,为了解决全球能源危机和环境污染日益严重的问题,越来越多的可再生能源并入到电网中,同时对于接口变换器的要求也越来越高.其中级联H桥逆变器由于具有多电平的优势,能够使交流侧输出电压更接近正弦波,减小了滤波电感的体积,因此在储能并网逆变器中得到广泛应用[1 ⇓ -3 ] 并得到了国内外学者的广泛研究[4 ⇓ ⇓ ⇓ -8 ] . ...
Power balance optimization of cascaded H-bridge multilevel converters for large-scale photovoltaic integration
1
2016
... 近几年,为了解决全球能源危机和环境污染日益严重的问题,越来越多的可再生能源并入到电网中,同时对于接口变换器的要求也越来越高.其中级联H桥逆变器由于具有多电平的优势,能够使交流侧输出电压更接近正弦波,减小了滤波电感的体积,因此在储能并网逆变器中得到广泛应用[1 ⇓ -3 ] 并得到了国内外学者的广泛研究[4 ⇓ ⇓ ⇓ -8 ] . ...
Multilevel inverters:A survey of topologies,controls,and applications
1
2007
... 近几年,为了解决全球能源危机和环境污染日益严重的问题,越来越多的可再生能源并入到电网中,同时对于接口变换器的要求也越来越高.其中级联H桥逆变器由于具有多电平的优势,能够使交流侧输出电压更接近正弦波,减小了滤波电感的体积,因此在储能并网逆变器中得到广泛应用[1 ⇓ -3 ] 并得到了国内外学者的广泛研究[4 ⇓ ⇓ ⇓ -8 ] . ...
Multilevel inverter topologies for stand-alone PV systems
1
2008
... 近几年,为了解决全球能源危机和环境污染日益严重的问题,越来越多的可再生能源并入到电网中,同时对于接口变换器的要求也越来越高.其中级联H桥逆变器由于具有多电平的优势,能够使交流侧输出电压更接近正弦波,减小了滤波电感的体积,因此在储能并网逆变器中得到广泛应用[1 ⇓ -3 ] 并得到了国内外学者的广泛研究[4 ⇓ ⇓ ⇓ -8 ] . ...
A survey on cascaded multilevel inverters
1
2010
... 近几年,为了解决全球能源危机和环境污染日益严重的问题,越来越多的可再生能源并入到电网中,同时对于接口变换器的要求也越来越高.其中级联H桥逆变器由于具有多电平的优势,能够使交流侧输出电压更接近正弦波,减小了滤波电感的体积,因此在储能并网逆变器中得到广泛应用[1 ⇓ -3 ] 并得到了国内外学者的广泛研究[4 ⇓ ⇓ ⇓ -8 ] . ...
大容量链式电池储能功率调节系统控制策略
1
2012
... 近几年,为了解决全球能源危机和环境污染日益严重的问题,越来越多的可再生能源并入到电网中,同时对于接口变换器的要求也越来越高.其中级联H桥逆变器由于具有多电平的优势,能够使交流侧输出电压更接近正弦波,减小了滤波电感的体积,因此在储能并网逆变器中得到广泛应用[1 ⇓ -3 ] 并得到了国内外学者的广泛研究[4 ⇓ ⇓ ⇓ -8 ] . ...
Large-capacity chain battery energy storage power regulation system control strategy
1
2012
... 近几年,为了解决全球能源危机和环境污染日益严重的问题,越来越多的可再生能源并入到电网中,同时对于接口变换器的要求也越来越高.其中级联H桥逆变器由于具有多电平的优势,能够使交流侧输出电压更接近正弦波,减小了滤波电感的体积,因此在储能并网逆变器中得到广泛应用[1 ⇓ -3 ] 并得到了国内外学者的广泛研究[4 ⇓ ⇓ ⇓ -8 ] . ...
高压直挂储能功率变换技术与世界首例应用
2
2020
... 近几年,为了解决全球能源危机和环境污染日益严重的问题,越来越多的可再生能源并入到电网中,同时对于接口变换器的要求也越来越高.其中级联H桥逆变器由于具有多电平的优势,能够使交流侧输出电压更接近正弦波,减小了滤波电感的体积,因此在储能并网逆变器中得到广泛应用[1 ⇓ -3 ] 并得到了国内外学者的广泛研究[4 ⇓ ⇓ ⇓ -8 ] . ...
... 为了说明在非理想电网条件下,本文所提出的控制方法以及本文提出的对于控制器参数设计方法的有效性与优势.对比仿真分析了文献[7 ]和文献[13 ]提出的采用比例积分控制器和比例谐振控制器来提高级联H桥输出电流质量的方法,其中图12 和图13 为电网电压在非理想状态时分别采用PI和PR控制器以及采用文献中的控制器参数设计方法所得到的仿真波形图,其中电网电压非理想状态主要体现在a相电压上升为原来的1.1倍,c相电压跌落为原来的0.9倍,同时三相电网电压中分别出现表2 中的谐波电压. ...
High-voltage direct-mounted energy storage power conversion technology and the world’s first application
2
2020
... 近几年,为了解决全球能源危机和环境污染日益严重的问题,越来越多的可再生能源并入到电网中,同时对于接口变换器的要求也越来越高.其中级联H桥逆变器由于具有多电平的优势,能够使交流侧输出电压更接近正弦波,减小了滤波电感的体积,因此在储能并网逆变器中得到广泛应用[1 ⇓ -3 ] 并得到了国内外学者的广泛研究[4 ⇓ ⇓ ⇓ -8 ] . ...
... 为了说明在非理想电网条件下,本文所提出的控制方法以及本文提出的对于控制器参数设计方法的有效性与优势.对比仿真分析了文献[7 ]和文献[13 ]提出的采用比例积分控制器和比例谐振控制器来提高级联H桥输出电流质量的方法,其中图12 和图13 为电网电压在非理想状态时分别采用PI和PR控制器以及采用文献中的控制器参数设计方法所得到的仿真波形图,其中电网电压非理想状态主要体现在a相电压上升为原来的1.1倍,c相电压跌落为原来的0.9倍,同时三相电网电压中分别出现表2 中的谐波电压. ...
Generalized theory of phase-shifted carrier pwm for cascaded H-bridge converters and modular multilevel converters
1
2016
... 近几年,为了解决全球能源危机和环境污染日益严重的问题,越来越多的可再生能源并入到电网中,同时对于接口变换器的要求也越来越高.其中级联H桥逆变器由于具有多电平的优势,能够使交流侧输出电压更接近正弦波,减小了滤波电感的体积,因此在储能并网逆变器中得到广泛应用[1 ⇓ -3 ] 并得到了国内外学者的广泛研究[4 ⇓ ⇓ ⇓ -8 ] . ...
不对称电网电压下光伏并网逆变器控制策略研究
1
2017
... 随着越来越多的新能源接入电网,电网电压中处于不平衡以及含有谐波等非理想状态是不可避免的,当电网电压处于非理想状态时,受到电网电压负序和谐波分量的影响,传统控制策略下的并网逆变器输出电流将会发生畸变,低次谐波含量高以及产生输出功率波动等问题,使逆变器和电网的运行情况恶化.为了解决电网电压处于非理想状态时传统控制策略下的并网逆变器所出现的问题,文献[9 ⇓ ⇓ ⇓ -13 ]提出的控制策略在dq 坐标系下采用比例积分(Proportional integral,PI)控制器和αβ 坐标系下采用比例谐振(Proportional resonance,PR)控制器来对并网电流进行控制.但是,当电网电压不可避免地会发生畸变导致电网电压中含有低次谐波分量时,采用比例积分控制方法会导致并网电流含有相应的谐波分量,进而导致并网电流含有较大的低次谐波分量;采用比例谐振控制方法虽然能够有效地抑制并网电流中的低次谐波分量,但是当电网处 于不平衡时会导致输出电流不平衡.文献[14 -15 ]提出基于双序前馈解耦的重复控制和比例积分控制器相结合的控制方法,在电网电压处于非理想状态时,虽然在一定程度上相比于单独的PI控制器能够减小并网电流的谐波含量,但是当电网电压中含有低次谐波分量时,该方法并不能有效地降低由此引起的并网电流中的低次谐波含量,文献[16 ]提出利用比例积分谐振控制器来消除由网侧电压畸变引起的单相变流器交流电流中的低次谐波,但是该文献中对于参数整定的过程较为模糊且无法得出控制器参数具体的选择范围,没有明确的约束规则,使得系统无法工作在较为理想的状态.文献[17 ⇓ -19 ]提出一种有限集模型预测控制,实现电网不平衡下并网控制,该方法不需要复杂的调制策略,但是为了满足并网要求,需要较大的总谐波失真(Total harmonic distortion,THD),因此会增加系统成本.文献[20 ]针对低次谐波抑制问题,提出基于自适应陷波器的谐波抑制方法.通过在主电流环中加入基于自适应陷波器的谐波抑制策略,可同时抑制多次谐波电流,具有控制结构简单的优点,取得了较好的效果.但其采用的自适应算法较复杂,其中步长参数选择会对算法收敛性影响较大从而影响谐波补偿效果. ...
Research on control strategy of photovoltaic grid-connected inverter under asymmetric grid voltage
1
2017
... 随着越来越多的新能源接入电网,电网电压中处于不平衡以及含有谐波等非理想状态是不可避免的,当电网电压处于非理想状态时,受到电网电压负序和谐波分量的影响,传统控制策略下的并网逆变器输出电流将会发生畸变,低次谐波含量高以及产生输出功率波动等问题,使逆变器和电网的运行情况恶化.为了解决电网电压处于非理想状态时传统控制策略下的并网逆变器所出现的问题,文献[9 ⇓ ⇓ ⇓ -13 ]提出的控制策略在dq 坐标系下采用比例积分(Proportional integral,PI)控制器和αβ 坐标系下采用比例谐振(Proportional resonance,PR)控制器来对并网电流进行控制.但是,当电网电压不可避免地会发生畸变导致电网电压中含有低次谐波分量时,采用比例积分控制方法会导致并网电流含有相应的谐波分量,进而导致并网电流含有较大的低次谐波分量;采用比例谐振控制方法虽然能够有效地抑制并网电流中的低次谐波分量,但是当电网处 于不平衡时会导致输出电流不平衡.文献[14 -15 ]提出基于双序前馈解耦的重复控制和比例积分控制器相结合的控制方法,在电网电压处于非理想状态时,虽然在一定程度上相比于单独的PI控制器能够减小并网电流的谐波含量,但是当电网电压中含有低次谐波分量时,该方法并不能有效地降低由此引起的并网电流中的低次谐波含量,文献[16 ]提出利用比例积分谐振控制器来消除由网侧电压畸变引起的单相变流器交流电流中的低次谐波,但是该文献中对于参数整定的过程较为模糊且无法得出控制器参数具体的选择范围,没有明确的约束规则,使得系统无法工作在较为理想的状态.文献[17 ⇓ -19 ]提出一种有限集模型预测控制,实现电网不平衡下并网控制,该方法不需要复杂的调制策略,但是为了满足并网要求,需要较大的总谐波失真(Total harmonic distortion,THD),因此会增加系统成本.文献[20 ]针对低次谐波抑制问题,提出基于自适应陷波器的谐波抑制方法.通过在主电流环中加入基于自适应陷波器的谐波抑制策略,可同时抑制多次谐波电流,具有控制结构简单的优点,取得了较好的效果.但其采用的自适应算法较复杂,其中步长参数选择会对算法收敛性影响较大从而影响谐波补偿效果. ...
A three-phase frequency-adaptive phase-locked loop for independent single-phase operation
1
2014
... 随着越来越多的新能源接入电网,电网电压中处于不平衡以及含有谐波等非理想状态是不可避免的,当电网电压处于非理想状态时,受到电网电压负序和谐波分量的影响,传统控制策略下的并网逆变器输出电流将会发生畸变,低次谐波含量高以及产生输出功率波动等问题,使逆变器和电网的运行情况恶化.为了解决电网电压处于非理想状态时传统控制策略下的并网逆变器所出现的问题,文献[9 ⇓ ⇓ ⇓ -13 ]提出的控制策略在dq 坐标系下采用比例积分(Proportional integral,PI)控制器和αβ 坐标系下采用比例谐振(Proportional resonance,PR)控制器来对并网电流进行控制.但是,当电网电压不可避免地会发生畸变导致电网电压中含有低次谐波分量时,采用比例积分控制方法会导致并网电流含有相应的谐波分量,进而导致并网电流含有较大的低次谐波分量;采用比例谐振控制方法虽然能够有效地抑制并网电流中的低次谐波分量,但是当电网处 于不平衡时会导致输出电流不平衡.文献[14 -15 ]提出基于双序前馈解耦的重复控制和比例积分控制器相结合的控制方法,在电网电压处于非理想状态时,虽然在一定程度上相比于单独的PI控制器能够减小并网电流的谐波含量,但是当电网电压中含有低次谐波分量时,该方法并不能有效地降低由此引起的并网电流中的低次谐波含量,文献[16 ]提出利用比例积分谐振控制器来消除由网侧电压畸变引起的单相变流器交流电流中的低次谐波,但是该文献中对于参数整定的过程较为模糊且无法得出控制器参数具体的选择范围,没有明确的约束规则,使得系统无法工作在较为理想的状态.文献[17 ⇓ -19 ]提出一种有限集模型预测控制,实现电网不平衡下并网控制,该方法不需要复杂的调制策略,但是为了满足并网要求,需要较大的总谐波失真(Total harmonic distortion,THD),因此会增加系统成本.文献[20 ]针对低次谐波抑制问题,提出基于自适应陷波器的谐波抑制方法.通过在主电流环中加入基于自适应陷波器的谐波抑制策略,可同时抑制多次谐波电流,具有控制结构简单的优点,取得了较好的效果.但其采用的自适应算法较复杂,其中步长参数选择会对算法收敛性影响较大从而影响谐波补偿效果. ...
单相并网逆变器准比例谐振控制器的设计
1
2012
... 随着越来越多的新能源接入电网,电网电压中处于不平衡以及含有谐波等非理想状态是不可避免的,当电网电压处于非理想状态时,受到电网电压负序和谐波分量的影响,传统控制策略下的并网逆变器输出电流将会发生畸变,低次谐波含量高以及产生输出功率波动等问题,使逆变器和电网的运行情况恶化.为了解决电网电压处于非理想状态时传统控制策略下的并网逆变器所出现的问题,文献[9 ⇓ ⇓ ⇓ -13 ]提出的控制策略在dq 坐标系下采用比例积分(Proportional integral,PI)控制器和αβ 坐标系下采用比例谐振(Proportional resonance,PR)控制器来对并网电流进行控制.但是,当电网电压不可避免地会发生畸变导致电网电压中含有低次谐波分量时,采用比例积分控制方法会导致并网电流含有相应的谐波分量,进而导致并网电流含有较大的低次谐波分量;采用比例谐振控制方法虽然能够有效地抑制并网电流中的低次谐波分量,但是当电网处 于不平衡时会导致输出电流不平衡.文献[14 -15 ]提出基于双序前馈解耦的重复控制和比例积分控制器相结合的控制方法,在电网电压处于非理想状态时,虽然在一定程度上相比于单独的PI控制器能够减小并网电流的谐波含量,但是当电网电压中含有低次谐波分量时,该方法并不能有效地降低由此引起的并网电流中的低次谐波含量,文献[16 ]提出利用比例积分谐振控制器来消除由网侧电压畸变引起的单相变流器交流电流中的低次谐波,但是该文献中对于参数整定的过程较为模糊且无法得出控制器参数具体的选择范围,没有明确的约束规则,使得系统无法工作在较为理想的状态.文献[17 ⇓ -19 ]提出一种有限集模型预测控制,实现电网不平衡下并网控制,该方法不需要复杂的调制策略,但是为了满足并网要求,需要较大的总谐波失真(Total harmonic distortion,THD),因此会增加系统成本.文献[20 ]针对低次谐波抑制问题,提出基于自适应陷波器的谐波抑制方法.通过在主电流环中加入基于自适应陷波器的谐波抑制策略,可同时抑制多次谐波电流,具有控制结构简单的优点,取得了较好的效果.但其采用的自适应算法较复杂,其中步长参数选择会对算法收敛性影响较大从而影响谐波补偿效果. ...
Design of quasi-proportional resonant controller for single-phase grid-connected inverter
1
2012
... 随着越来越多的新能源接入电网,电网电压中处于不平衡以及含有谐波等非理想状态是不可避免的,当电网电压处于非理想状态时,受到电网电压负序和谐波分量的影响,传统控制策略下的并网逆变器输出电流将会发生畸变,低次谐波含量高以及产生输出功率波动等问题,使逆变器和电网的运行情况恶化.为了解决电网电压处于非理想状态时传统控制策略下的并网逆变器所出现的问题,文献[9 ⇓ ⇓ ⇓ -13 ]提出的控制策略在dq 坐标系下采用比例积分(Proportional integral,PI)控制器和αβ 坐标系下采用比例谐振(Proportional resonance,PR)控制器来对并网电流进行控制.但是,当电网电压不可避免地会发生畸变导致电网电压中含有低次谐波分量时,采用比例积分控制方法会导致并网电流含有相应的谐波分量,进而导致并网电流含有较大的低次谐波分量;采用比例谐振控制方法虽然能够有效地抑制并网电流中的低次谐波分量,但是当电网处 于不平衡时会导致输出电流不平衡.文献[14 -15 ]提出基于双序前馈解耦的重复控制和比例积分控制器相结合的控制方法,在电网电压处于非理想状态时,虽然在一定程度上相比于单独的PI控制器能够减小并网电流的谐波含量,但是当电网电压中含有低次谐波分量时,该方法并不能有效地降低由此引起的并网电流中的低次谐波含量,文献[16 ]提出利用比例积分谐振控制器来消除由网侧电压畸变引起的单相变流器交流电流中的低次谐波,但是该文献中对于参数整定的过程较为模糊且无法得出控制器参数具体的选择范围,没有明确的约束规则,使得系统无法工作在较为理想的状态.文献[17 ⇓ -19 ]提出一种有限集模型预测控制,实现电网不平衡下并网控制,该方法不需要复杂的调制策略,但是为了满足并网要求,需要较大的总谐波失真(Total harmonic distortion,THD),因此会增加系统成本.文献[20 ]针对低次谐波抑制问题,提出基于自适应陷波器的谐波抑制方法.通过在主电流环中加入基于自适应陷波器的谐波抑制策略,可同时抑制多次谐波电流,具有控制结构简单的优点,取得了较好的效果.但其采用的自适应算法较复杂,其中步长参数选择会对算法收敛性影响较大从而影响谐波补偿效果. ...
An enhanced grid current compensator for grid-connected distributed generation under nonlinear loads and grid voltage distortions
1
2014
... 随着越来越多的新能源接入电网,电网电压中处于不平衡以及含有谐波等非理想状态是不可避免的,当电网电压处于非理想状态时,受到电网电压负序和谐波分量的影响,传统控制策略下的并网逆变器输出电流将会发生畸变,低次谐波含量高以及产生输出功率波动等问题,使逆变器和电网的运行情况恶化.为了解决电网电压处于非理想状态时传统控制策略下的并网逆变器所出现的问题,文献[9 ⇓ ⇓ ⇓ -13 ]提出的控制策略在dq 坐标系下采用比例积分(Proportional integral,PI)控制器和αβ 坐标系下采用比例谐振(Proportional resonance,PR)控制器来对并网电流进行控制.但是,当电网电压不可避免地会发生畸变导致电网电压中含有低次谐波分量时,采用比例积分控制方法会导致并网电流含有相应的谐波分量,进而导致并网电流含有较大的低次谐波分量;采用比例谐振控制方法虽然能够有效地抑制并网电流中的低次谐波分量,但是当电网处 于不平衡时会导致输出电流不平衡.文献[14 -15 ]提出基于双序前馈解耦的重复控制和比例积分控制器相结合的控制方法,在电网电压处于非理想状态时,虽然在一定程度上相比于单独的PI控制器能够减小并网电流的谐波含量,但是当电网电压中含有低次谐波分量时,该方法并不能有效地降低由此引起的并网电流中的低次谐波含量,文献[16 ]提出利用比例积分谐振控制器来消除由网侧电压畸变引起的单相变流器交流电流中的低次谐波,但是该文献中对于参数整定的过程较为模糊且无法得出控制器参数具体的选择范围,没有明确的约束规则,使得系统无法工作在较为理想的状态.文献[17 ⇓ -19 ]提出一种有限集模型预测控制,实现电网不平衡下并网控制,该方法不需要复杂的调制策略,但是为了满足并网要求,需要较大的总谐波失真(Total harmonic distortion,THD),因此会增加系统成本.文献[20 ]针对低次谐波抑制问题,提出基于自适应陷波器的谐波抑制方法.通过在主电流环中加入基于自适应陷波器的谐波抑制策略,可同时抑制多次谐波电流,具有控制结构简单的优点,取得了较好的效果.但其采用的自适应算法较复杂,其中步长参数选择会对算法收敛性影响较大从而影响谐波补偿效果. ...
电网畸变级联H桥逆变器控制研究
2
2019
... 随着越来越多的新能源接入电网,电网电压中处于不平衡以及含有谐波等非理想状态是不可避免的,当电网电压处于非理想状态时,受到电网电压负序和谐波分量的影响,传统控制策略下的并网逆变器输出电流将会发生畸变,低次谐波含量高以及产生输出功率波动等问题,使逆变器和电网的运行情况恶化.为了解决电网电压处于非理想状态时传统控制策略下的并网逆变器所出现的问题,文献[9 ⇓ ⇓ ⇓ -13 ]提出的控制策略在dq 坐标系下采用比例积分(Proportional integral,PI)控制器和αβ 坐标系下采用比例谐振(Proportional resonance,PR)控制器来对并网电流进行控制.但是,当电网电压不可避免地会发生畸变导致电网电压中含有低次谐波分量时,采用比例积分控制方法会导致并网电流含有相应的谐波分量,进而导致并网电流含有较大的低次谐波分量;采用比例谐振控制方法虽然能够有效地抑制并网电流中的低次谐波分量,但是当电网处 于不平衡时会导致输出电流不平衡.文献[14 -15 ]提出基于双序前馈解耦的重复控制和比例积分控制器相结合的控制方法,在电网电压处于非理想状态时,虽然在一定程度上相比于单独的PI控制器能够减小并网电流的谐波含量,但是当电网电压中含有低次谐波分量时,该方法并不能有效地降低由此引起的并网电流中的低次谐波含量,文献[16 ]提出利用比例积分谐振控制器来消除由网侧电压畸变引起的单相变流器交流电流中的低次谐波,但是该文献中对于参数整定的过程较为模糊且无法得出控制器参数具体的选择范围,没有明确的约束规则,使得系统无法工作在较为理想的状态.文献[17 ⇓ -19 ]提出一种有限集模型预测控制,实现电网不平衡下并网控制,该方法不需要复杂的调制策略,但是为了满足并网要求,需要较大的总谐波失真(Total harmonic distortion,THD),因此会增加系统成本.文献[20 ]针对低次谐波抑制问题,提出基于自适应陷波器的谐波抑制方法.通过在主电流环中加入基于自适应陷波器的谐波抑制策略,可同时抑制多次谐波电流,具有控制结构简单的优点,取得了较好的效果.但其采用的自适应算法较复杂,其中步长参数选择会对算法收敛性影响较大从而影响谐波补偿效果. ...
... 为了说明在非理想电网条件下,本文所提出的控制方法以及本文提出的对于控制器参数设计方法的有效性与优势.对比仿真分析了文献[7 ]和文献[13 ]提出的采用比例积分控制器和比例谐振控制器来提高级联H桥输出电流质量的方法,其中图12 和图13 为电网电压在非理想状态时分别采用PI和PR控制器以及采用文献中的控制器参数设计方法所得到的仿真波形图,其中电网电压非理想状态主要体现在a相电压上升为原来的1.1倍,c相电压跌落为原来的0.9倍,同时三相电网电压中分别出现表2 中的谐波电压. ...
Research on the control of power grid distortion cascaded H-bridge inverter
2
2019
... 随着越来越多的新能源接入电网,电网电压中处于不平衡以及含有谐波等非理想状态是不可避免的,当电网电压处于非理想状态时,受到电网电压负序和谐波分量的影响,传统控制策略下的并网逆变器输出电流将会发生畸变,低次谐波含量高以及产生输出功率波动等问题,使逆变器和电网的运行情况恶化.为了解决电网电压处于非理想状态时传统控制策略下的并网逆变器所出现的问题,文献[9 ⇓ ⇓ ⇓ -13 ]提出的控制策略在dq 坐标系下采用比例积分(Proportional integral,PI)控制器和αβ 坐标系下采用比例谐振(Proportional resonance,PR)控制器来对并网电流进行控制.但是,当电网电压不可避免地会发生畸变导致电网电压中含有低次谐波分量时,采用比例积分控制方法会导致并网电流含有相应的谐波分量,进而导致并网电流含有较大的低次谐波分量;采用比例谐振控制方法虽然能够有效地抑制并网电流中的低次谐波分量,但是当电网处 于不平衡时会导致输出电流不平衡.文献[14 -15 ]提出基于双序前馈解耦的重复控制和比例积分控制器相结合的控制方法,在电网电压处于非理想状态时,虽然在一定程度上相比于单独的PI控制器能够减小并网电流的谐波含量,但是当电网电压中含有低次谐波分量时,该方法并不能有效地降低由此引起的并网电流中的低次谐波含量,文献[16 ]提出利用比例积分谐振控制器来消除由网侧电压畸变引起的单相变流器交流电流中的低次谐波,但是该文献中对于参数整定的过程较为模糊且无法得出控制器参数具体的选择范围,没有明确的约束规则,使得系统无法工作在较为理想的状态.文献[17 ⇓ -19 ]提出一种有限集模型预测控制,实现电网不平衡下并网控制,该方法不需要复杂的调制策略,但是为了满足并网要求,需要较大的总谐波失真(Total harmonic distortion,THD),因此会增加系统成本.文献[20 ]针对低次谐波抑制问题,提出基于自适应陷波器的谐波抑制方法.通过在主电流环中加入基于自适应陷波器的谐波抑制策略,可同时抑制多次谐波电流,具有控制结构简单的优点,取得了较好的效果.但其采用的自适应算法较复杂,其中步长参数选择会对算法收敛性影响较大从而影响谐波补偿效果. ...
... 为了说明在非理想电网条件下,本文所提出的控制方法以及本文提出的对于控制器参数设计方法的有效性与优势.对比仿真分析了文献[7 ]和文献[13 ]提出的采用比例积分控制器和比例谐振控制器来提高级联H桥输出电流质量的方法,其中图12 和图13 为电网电压在非理想状态时分别采用PI和PR控制器以及采用文献中的控制器参数设计方法所得到的仿真波形图,其中电网电压非理想状态主要体现在a相电压上升为原来的1.1倍,c相电压跌落为原来的0.9倍,同时三相电网电压中分别出现表2 中的谐波电压. ...
基于双序前馈解耦的光伏逆变器并网控制策略
1
2021
... 随着越来越多的新能源接入电网,电网电压中处于不平衡以及含有谐波等非理想状态是不可避免的,当电网电压处于非理想状态时,受到电网电压负序和谐波分量的影响,传统控制策略下的并网逆变器输出电流将会发生畸变,低次谐波含量高以及产生输出功率波动等问题,使逆变器和电网的运行情况恶化.为了解决电网电压处于非理想状态时传统控制策略下的并网逆变器所出现的问题,文献[9 ⇓ ⇓ ⇓ -13 ]提出的控制策略在dq 坐标系下采用比例积分(Proportional integral,PI)控制器和αβ 坐标系下采用比例谐振(Proportional resonance,PR)控制器来对并网电流进行控制.但是,当电网电压不可避免地会发生畸变导致电网电压中含有低次谐波分量时,采用比例积分控制方法会导致并网电流含有相应的谐波分量,进而导致并网电流含有较大的低次谐波分量;采用比例谐振控制方法虽然能够有效地抑制并网电流中的低次谐波分量,但是当电网处 于不平衡时会导致输出电流不平衡.文献[14 -15 ]提出基于双序前馈解耦的重复控制和比例积分控制器相结合的控制方法,在电网电压处于非理想状态时,虽然在一定程度上相比于单独的PI控制器能够减小并网电流的谐波含量,但是当电网电压中含有低次谐波分量时,该方法并不能有效地降低由此引起的并网电流中的低次谐波含量,文献[16 ]提出利用比例积分谐振控制器来消除由网侧电压畸变引起的单相变流器交流电流中的低次谐波,但是该文献中对于参数整定的过程较为模糊且无法得出控制器参数具体的选择范围,没有明确的约束规则,使得系统无法工作在较为理想的状态.文献[17 ⇓ -19 ]提出一种有限集模型预测控制,实现电网不平衡下并网控制,该方法不需要复杂的调制策略,但是为了满足并网要求,需要较大的总谐波失真(Total harmonic distortion,THD),因此会增加系统成本.文献[20 ]针对低次谐波抑制问题,提出基于自适应陷波器的谐波抑制方法.通过在主电流环中加入基于自适应陷波器的谐波抑制策略,可同时抑制多次谐波电流,具有控制结构简单的优点,取得了较好的效果.但其采用的自适应算法较复杂,其中步长参数选择会对算法收敛性影响较大从而影响谐波补偿效果. ...
Grid-connected photovoltaic inverter control strategy based on double-sequence feedforward decoupling
1
2021
... 随着越来越多的新能源接入电网,电网电压中处于不平衡以及含有谐波等非理想状态是不可避免的,当电网电压处于非理想状态时,受到电网电压负序和谐波分量的影响,传统控制策略下的并网逆变器输出电流将会发生畸变,低次谐波含量高以及产生输出功率波动等问题,使逆变器和电网的运行情况恶化.为了解决电网电压处于非理想状态时传统控制策略下的并网逆变器所出现的问题,文献[9 ⇓ ⇓ ⇓ -13 ]提出的控制策略在dq 坐标系下采用比例积分(Proportional integral,PI)控制器和αβ 坐标系下采用比例谐振(Proportional resonance,PR)控制器来对并网电流进行控制.但是,当电网电压不可避免地会发生畸变导致电网电压中含有低次谐波分量时,采用比例积分控制方法会导致并网电流含有相应的谐波分量,进而导致并网电流含有较大的低次谐波分量;采用比例谐振控制方法虽然能够有效地抑制并网电流中的低次谐波分量,但是当电网处 于不平衡时会导致输出电流不平衡.文献[14 -15 ]提出基于双序前馈解耦的重复控制和比例积分控制器相结合的控制方法,在电网电压处于非理想状态时,虽然在一定程度上相比于单独的PI控制器能够减小并网电流的谐波含量,但是当电网电压中含有低次谐波分量时,该方法并不能有效地降低由此引起的并网电流中的低次谐波含量,文献[16 ]提出利用比例积分谐振控制器来消除由网侧电压畸变引起的单相变流器交流电流中的低次谐波,但是该文献中对于参数整定的过程较为模糊且无法得出控制器参数具体的选择范围,没有明确的约束规则,使得系统无法工作在较为理想的状态.文献[17 ⇓ -19 ]提出一种有限集模型预测控制,实现电网不平衡下并网控制,该方法不需要复杂的调制策略,但是为了满足并网要求,需要较大的总谐波失真(Total harmonic distortion,THD),因此会增加系统成本.文献[20 ]针对低次谐波抑制问题,提出基于自适应陷波器的谐波抑制方法.通过在主电流环中加入基于自适应陷波器的谐波抑制策略,可同时抑制多次谐波电流,具有控制结构简单的优点,取得了较好的效果.但其采用的自适应算法较复杂,其中步长参数选择会对算法收敛性影响较大从而影响谐波补偿效果. ...
Deadbeat control based on current predictive calibration for grid-connected converter under unbalanced grid voltage
1
2017
... 随着越来越多的新能源接入电网,电网电压中处于不平衡以及含有谐波等非理想状态是不可避免的,当电网电压处于非理想状态时,受到电网电压负序和谐波分量的影响,传统控制策略下的并网逆变器输出电流将会发生畸变,低次谐波含量高以及产生输出功率波动等问题,使逆变器和电网的运行情况恶化.为了解决电网电压处于非理想状态时传统控制策略下的并网逆变器所出现的问题,文献[9 ⇓ ⇓ ⇓ -13 ]提出的控制策略在dq 坐标系下采用比例积分(Proportional integral,PI)控制器和αβ 坐标系下采用比例谐振(Proportional resonance,PR)控制器来对并网电流进行控制.但是,当电网电压不可避免地会发生畸变导致电网电压中含有低次谐波分量时,采用比例积分控制方法会导致并网电流含有相应的谐波分量,进而导致并网电流含有较大的低次谐波分量;采用比例谐振控制方法虽然能够有效地抑制并网电流中的低次谐波分量,但是当电网处 于不平衡时会导致输出电流不平衡.文献[14 -15 ]提出基于双序前馈解耦的重复控制和比例积分控制器相结合的控制方法,在电网电压处于非理想状态时,虽然在一定程度上相比于单独的PI控制器能够减小并网电流的谐波含量,但是当电网电压中含有低次谐波分量时,该方法并不能有效地降低由此引起的并网电流中的低次谐波含量,文献[16 ]提出利用比例积分谐振控制器来消除由网侧电压畸变引起的单相变流器交流电流中的低次谐波,但是该文献中对于参数整定的过程较为模糊且无法得出控制器参数具体的选择范围,没有明确的约束规则,使得系统无法工作在较为理想的状态.文献[17 ⇓ -19 ]提出一种有限集模型预测控制,实现电网不平衡下并网控制,该方法不需要复杂的调制策略,但是为了满足并网要求,需要较大的总谐波失真(Total harmonic distortion,THD),因此会增加系统成本.文献[20 ]针对低次谐波抑制问题,提出基于自适应陷波器的谐波抑制方法.通过在主电流环中加入基于自适应陷波器的谐波抑制策略,可同时抑制多次谐波电流,具有控制结构简单的优点,取得了较好的效果.但其采用的自适应算法较复杂,其中步长参数选择会对算法收敛性影响较大从而影响谐波补偿效果. ...
具有低次谐波抑制能力的PIR控制器设计
1
2016
... 随着越来越多的新能源接入电网,电网电压中处于不平衡以及含有谐波等非理想状态是不可避免的,当电网电压处于非理想状态时,受到电网电压负序和谐波分量的影响,传统控制策略下的并网逆变器输出电流将会发生畸变,低次谐波含量高以及产生输出功率波动等问题,使逆变器和电网的运行情况恶化.为了解决电网电压处于非理想状态时传统控制策略下的并网逆变器所出现的问题,文献[9 ⇓ ⇓ ⇓ -13 ]提出的控制策略在dq 坐标系下采用比例积分(Proportional integral,PI)控制器和αβ 坐标系下采用比例谐振(Proportional resonance,PR)控制器来对并网电流进行控制.但是,当电网电压不可避免地会发生畸变导致电网电压中含有低次谐波分量时,采用比例积分控制方法会导致并网电流含有相应的谐波分量,进而导致并网电流含有较大的低次谐波分量;采用比例谐振控制方法虽然能够有效地抑制并网电流中的低次谐波分量,但是当电网处 于不平衡时会导致输出电流不平衡.文献[14 -15 ]提出基于双序前馈解耦的重复控制和比例积分控制器相结合的控制方法,在电网电压处于非理想状态时,虽然在一定程度上相比于单独的PI控制器能够减小并网电流的谐波含量,但是当电网电压中含有低次谐波分量时,该方法并不能有效地降低由此引起的并网电流中的低次谐波含量,文献[16 ]提出利用比例积分谐振控制器来消除由网侧电压畸变引起的单相变流器交流电流中的低次谐波,但是该文献中对于参数整定的过程较为模糊且无法得出控制器参数具体的选择范围,没有明确的约束规则,使得系统无法工作在较为理想的状态.文献[17 ⇓ -19 ]提出一种有限集模型预测控制,实现电网不平衡下并网控制,该方法不需要复杂的调制策略,但是为了满足并网要求,需要较大的总谐波失真(Total harmonic distortion,THD),因此会增加系统成本.文献[20 ]针对低次谐波抑制问题,提出基于自适应陷波器的谐波抑制方法.通过在主电流环中加入基于自适应陷波器的谐波抑制策略,可同时抑制多次谐波电流,具有控制结构简单的优点,取得了较好的效果.但其采用的自适应算法较复杂,其中步长参数选择会对算法收敛性影响较大从而影响谐波补偿效果. ...
Design of PIR controller with low-order harmonic suppression ability
1
2016
... 随着越来越多的新能源接入电网,电网电压中处于不平衡以及含有谐波等非理想状态是不可避免的,当电网电压处于非理想状态时,受到电网电压负序和谐波分量的影响,传统控制策略下的并网逆变器输出电流将会发生畸变,低次谐波含量高以及产生输出功率波动等问题,使逆变器和电网的运行情况恶化.为了解决电网电压处于非理想状态时传统控制策略下的并网逆变器所出现的问题,文献[9 ⇓ ⇓ ⇓ -13 ]提出的控制策略在dq 坐标系下采用比例积分(Proportional integral,PI)控制器和αβ 坐标系下采用比例谐振(Proportional resonance,PR)控制器来对并网电流进行控制.但是,当电网电压不可避免地会发生畸变导致电网电压中含有低次谐波分量时,采用比例积分控制方法会导致并网电流含有相应的谐波分量,进而导致并网电流含有较大的低次谐波分量;采用比例谐振控制方法虽然能够有效地抑制并网电流中的低次谐波分量,但是当电网处 于不平衡时会导致输出电流不平衡.文献[14 -15 ]提出基于双序前馈解耦的重复控制和比例积分控制器相结合的控制方法,在电网电压处于非理想状态时,虽然在一定程度上相比于单独的PI控制器能够减小并网电流的谐波含量,但是当电网电压中含有低次谐波分量时,该方法并不能有效地降低由此引起的并网电流中的低次谐波含量,文献[16 ]提出利用比例积分谐振控制器来消除由网侧电压畸变引起的单相变流器交流电流中的低次谐波,但是该文献中对于参数整定的过程较为模糊且无法得出控制器参数具体的选择范围,没有明确的约束规则,使得系统无法工作在较为理想的状态.文献[17 ⇓ -19 ]提出一种有限集模型预测控制,实现电网不平衡下并网控制,该方法不需要复杂的调制策略,但是为了满足并网要求,需要较大的总谐波失真(Total harmonic distortion,THD),因此会增加系统成本.文献[20 ]针对低次谐波抑制问题,提出基于自适应陷波器的谐波抑制方法.通过在主电流环中加入基于自适应陷波器的谐波抑制策略,可同时抑制多次谐波电流,具有控制结构简单的优点,取得了较好的效果.但其采用的自适应算法较复杂,其中步长参数选择会对算法收敛性影响较大从而影响谐波补偿效果. ...
Predictive control of cascaded H-bridge converters under unbalanced power generation
1
2017
... 随着越来越多的新能源接入电网,电网电压中处于不平衡以及含有谐波等非理想状态是不可避免的,当电网电压处于非理想状态时,受到电网电压负序和谐波分量的影响,传统控制策略下的并网逆变器输出电流将会发生畸变,低次谐波含量高以及产生输出功率波动等问题,使逆变器和电网的运行情况恶化.为了解决电网电压处于非理想状态时传统控制策略下的并网逆变器所出现的问题,文献[9 ⇓ ⇓ ⇓ -13 ]提出的控制策略在dq 坐标系下采用比例积分(Proportional integral,PI)控制器和αβ 坐标系下采用比例谐振(Proportional resonance,PR)控制器来对并网电流进行控制.但是,当电网电压不可避免地会发生畸变导致电网电压中含有低次谐波分量时,采用比例积分控制方法会导致并网电流含有相应的谐波分量,进而导致并网电流含有较大的低次谐波分量;采用比例谐振控制方法虽然能够有效地抑制并网电流中的低次谐波分量,但是当电网处 于不平衡时会导致输出电流不平衡.文献[14 -15 ]提出基于双序前馈解耦的重复控制和比例积分控制器相结合的控制方法,在电网电压处于非理想状态时,虽然在一定程度上相比于单独的PI控制器能够减小并网电流的谐波含量,但是当电网电压中含有低次谐波分量时,该方法并不能有效地降低由此引起的并网电流中的低次谐波含量,文献[16 ]提出利用比例积分谐振控制器来消除由网侧电压畸变引起的单相变流器交流电流中的低次谐波,但是该文献中对于参数整定的过程较为模糊且无法得出控制器参数具体的选择范围,没有明确的约束规则,使得系统无法工作在较为理想的状态.文献[17 ⇓ -19 ]提出一种有限集模型预测控制,实现电网不平衡下并网控制,该方法不需要复杂的调制策略,但是为了满足并网要求,需要较大的总谐波失真(Total harmonic distortion,THD),因此会增加系统成本.文献[20 ]针对低次谐波抑制问题,提出基于自适应陷波器的谐波抑制方法.通过在主电流环中加入基于自适应陷波器的谐波抑制策略,可同时抑制多次谐波电流,具有控制结构简单的优点,取得了较好的效果.但其采用的自适应算法较复杂,其中步长参数选择会对算法收敛性影响较大从而影响谐波补偿效果. ...
多电平级联H桥逆变器的模型预测控制策略
1
2021
... 随着越来越多的新能源接入电网,电网电压中处于不平衡以及含有谐波等非理想状态是不可避免的,当电网电压处于非理想状态时,受到电网电压负序和谐波分量的影响,传统控制策略下的并网逆变器输出电流将会发生畸变,低次谐波含量高以及产生输出功率波动等问题,使逆变器和电网的运行情况恶化.为了解决电网电压处于非理想状态时传统控制策略下的并网逆变器所出现的问题,文献[9 ⇓ ⇓ ⇓ -13 ]提出的控制策略在dq 坐标系下采用比例积分(Proportional integral,PI)控制器和αβ 坐标系下采用比例谐振(Proportional resonance,PR)控制器来对并网电流进行控制.但是,当电网电压不可避免地会发生畸变导致电网电压中含有低次谐波分量时,采用比例积分控制方法会导致并网电流含有相应的谐波分量,进而导致并网电流含有较大的低次谐波分量;采用比例谐振控制方法虽然能够有效地抑制并网电流中的低次谐波分量,但是当电网处 于不平衡时会导致输出电流不平衡.文献[14 -15 ]提出基于双序前馈解耦的重复控制和比例积分控制器相结合的控制方法,在电网电压处于非理想状态时,虽然在一定程度上相比于单独的PI控制器能够减小并网电流的谐波含量,但是当电网电压中含有低次谐波分量时,该方法并不能有效地降低由此引起的并网电流中的低次谐波含量,文献[16 ]提出利用比例积分谐振控制器来消除由网侧电压畸变引起的单相变流器交流电流中的低次谐波,但是该文献中对于参数整定的过程较为模糊且无法得出控制器参数具体的选择范围,没有明确的约束规则,使得系统无法工作在较为理想的状态.文献[17 ⇓ -19 ]提出一种有限集模型预测控制,实现电网不平衡下并网控制,该方法不需要复杂的调制策略,但是为了满足并网要求,需要较大的总谐波失真(Total harmonic distortion,THD),因此会增加系统成本.文献[20 ]针对低次谐波抑制问题,提出基于自适应陷波器的谐波抑制方法.通过在主电流环中加入基于自适应陷波器的谐波抑制策略,可同时抑制多次谐波电流,具有控制结构简单的优点,取得了较好的效果.但其采用的自适应算法较复杂,其中步长参数选择会对算法收敛性影响较大从而影响谐波补偿效果. ...
Model predictive control strategy for multi-level cascaded H-bridge inverters
1
2021
... 随着越来越多的新能源接入电网,电网电压中处于不平衡以及含有谐波等非理想状态是不可避免的,当电网电压处于非理想状态时,受到电网电压负序和谐波分量的影响,传统控制策略下的并网逆变器输出电流将会发生畸变,低次谐波含量高以及产生输出功率波动等问题,使逆变器和电网的运行情况恶化.为了解决电网电压处于非理想状态时传统控制策略下的并网逆变器所出现的问题,文献[9 ⇓ ⇓ ⇓ -13 ]提出的控制策略在dq 坐标系下采用比例积分(Proportional integral,PI)控制器和αβ 坐标系下采用比例谐振(Proportional resonance,PR)控制器来对并网电流进行控制.但是,当电网电压不可避免地会发生畸变导致电网电压中含有低次谐波分量时,采用比例积分控制方法会导致并网电流含有相应的谐波分量,进而导致并网电流含有较大的低次谐波分量;采用比例谐振控制方法虽然能够有效地抑制并网电流中的低次谐波分量,但是当电网处 于不平衡时会导致输出电流不平衡.文献[14 -15 ]提出基于双序前馈解耦的重复控制和比例积分控制器相结合的控制方法,在电网电压处于非理想状态时,虽然在一定程度上相比于单独的PI控制器能够减小并网电流的谐波含量,但是当电网电压中含有低次谐波分量时,该方法并不能有效地降低由此引起的并网电流中的低次谐波含量,文献[16 ]提出利用比例积分谐振控制器来消除由网侧电压畸变引起的单相变流器交流电流中的低次谐波,但是该文献中对于参数整定的过程较为模糊且无法得出控制器参数具体的选择范围,没有明确的约束规则,使得系统无法工作在较为理想的状态.文献[17 ⇓ -19 ]提出一种有限集模型预测控制,实现电网不平衡下并网控制,该方法不需要复杂的调制策略,但是为了满足并网要求,需要较大的总谐波失真(Total harmonic distortion,THD),因此会增加系统成本.文献[20 ]针对低次谐波抑制问题,提出基于自适应陷波器的谐波抑制方法.通过在主电流环中加入基于自适应陷波器的谐波抑制策略,可同时抑制多次谐波电流,具有控制结构简单的优点,取得了较好的效果.但其采用的自适应算法较复杂,其中步长参数选择会对算法收敛性影响较大从而影响谐波补偿效果. ...
不平衡电网下并网逆变器的模型预测电流限幅灵活控制
1
2019
... 随着越来越多的新能源接入电网,电网电压中处于不平衡以及含有谐波等非理想状态是不可避免的,当电网电压处于非理想状态时,受到电网电压负序和谐波分量的影响,传统控制策略下的并网逆变器输出电流将会发生畸变,低次谐波含量高以及产生输出功率波动等问题,使逆变器和电网的运行情况恶化.为了解决电网电压处于非理想状态时传统控制策略下的并网逆变器所出现的问题,文献[9 ⇓ ⇓ ⇓ -13 ]提出的控制策略在dq 坐标系下采用比例积分(Proportional integral,PI)控制器和αβ 坐标系下采用比例谐振(Proportional resonance,PR)控制器来对并网电流进行控制.但是,当电网电压不可避免地会发生畸变导致电网电压中含有低次谐波分量时,采用比例积分控制方法会导致并网电流含有相应的谐波分量,进而导致并网电流含有较大的低次谐波分量;采用比例谐振控制方法虽然能够有效地抑制并网电流中的低次谐波分量,但是当电网处 于不平衡时会导致输出电流不平衡.文献[14 -15 ]提出基于双序前馈解耦的重复控制和比例积分控制器相结合的控制方法,在电网电压处于非理想状态时,虽然在一定程度上相比于单独的PI控制器能够减小并网电流的谐波含量,但是当电网电压中含有低次谐波分量时,该方法并不能有效地降低由此引起的并网电流中的低次谐波含量,文献[16 ]提出利用比例积分谐振控制器来消除由网侧电压畸变引起的单相变流器交流电流中的低次谐波,但是该文献中对于参数整定的过程较为模糊且无法得出控制器参数具体的选择范围,没有明确的约束规则,使得系统无法工作在较为理想的状态.文献[17 ⇓ -19 ]提出一种有限集模型预测控制,实现电网不平衡下并网控制,该方法不需要复杂的调制策略,但是为了满足并网要求,需要较大的总谐波失真(Total harmonic distortion,THD),因此会增加系统成本.文献[20 ]针对低次谐波抑制问题,提出基于自适应陷波器的谐波抑制方法.通过在主电流环中加入基于自适应陷波器的谐波抑制策略,可同时抑制多次谐波电流,具有控制结构简单的优点,取得了较好的效果.但其采用的自适应算法较复杂,其中步长参数选择会对算法收敛性影响较大从而影响谐波补偿效果. ...
Model-predicted current limiting flexible control of grid-connected inverters in unbalanced grids
1
2019
... 随着越来越多的新能源接入电网,电网电压中处于不平衡以及含有谐波等非理想状态是不可避免的,当电网电压处于非理想状态时,受到电网电压负序和谐波分量的影响,传统控制策略下的并网逆变器输出电流将会发生畸变,低次谐波含量高以及产生输出功率波动等问题,使逆变器和电网的运行情况恶化.为了解决电网电压处于非理想状态时传统控制策略下的并网逆变器所出现的问题,文献[9 ⇓ ⇓ ⇓ -13 ]提出的控制策略在dq 坐标系下采用比例积分(Proportional integral,PI)控制器和αβ 坐标系下采用比例谐振(Proportional resonance,PR)控制器来对并网电流进行控制.但是,当电网电压不可避免地会发生畸变导致电网电压中含有低次谐波分量时,采用比例积分控制方法会导致并网电流含有相应的谐波分量,进而导致并网电流含有较大的低次谐波分量;采用比例谐振控制方法虽然能够有效地抑制并网电流中的低次谐波分量,但是当电网处 于不平衡时会导致输出电流不平衡.文献[14 -15 ]提出基于双序前馈解耦的重复控制和比例积分控制器相结合的控制方法,在电网电压处于非理想状态时,虽然在一定程度上相比于单独的PI控制器能够减小并网电流的谐波含量,但是当电网电压中含有低次谐波分量时,该方法并不能有效地降低由此引起的并网电流中的低次谐波含量,文献[16 ]提出利用比例积分谐振控制器来消除由网侧电压畸变引起的单相变流器交流电流中的低次谐波,但是该文献中对于参数整定的过程较为模糊且无法得出控制器参数具体的选择范围,没有明确的约束规则,使得系统无法工作在较为理想的状态.文献[17 ⇓ -19 ]提出一种有限集模型预测控制,实现电网不平衡下并网控制,该方法不需要复杂的调制策略,但是为了满足并网要求,需要较大的总谐波失真(Total harmonic distortion,THD),因此会增加系统成本.文献[20 ]针对低次谐波抑制问题,提出基于自适应陷波器的谐波抑制方法.通过在主电流环中加入基于自适应陷波器的谐波抑制策略,可同时抑制多次谐波电流,具有控制结构简单的优点,取得了较好的效果.但其采用的自适应算法较复杂,其中步长参数选择会对算法收敛性影响较大从而影响谐波补偿效果. ...
1
2014
... 随着越来越多的新能源接入电网,电网电压中处于不平衡以及含有谐波等非理想状态是不可避免的,当电网电压处于非理想状态时,受到电网电压负序和谐波分量的影响,传统控制策略下的并网逆变器输出电流将会发生畸变,低次谐波含量高以及产生输出功率波动等问题,使逆变器和电网的运行情况恶化.为了解决电网电压处于非理想状态时传统控制策略下的并网逆变器所出现的问题,文献[9 ⇓ ⇓ ⇓ -13 ]提出的控制策略在dq 坐标系下采用比例积分(Proportional integral,PI)控制器和αβ 坐标系下采用比例谐振(Proportional resonance,PR)控制器来对并网电流进行控制.但是,当电网电压不可避免地会发生畸变导致电网电压中含有低次谐波分量时,采用比例积分控制方法会导致并网电流含有相应的谐波分量,进而导致并网电流含有较大的低次谐波分量;采用比例谐振控制方法虽然能够有效地抑制并网电流中的低次谐波分量,但是当电网处 于不平衡时会导致输出电流不平衡.文献[14 -15 ]提出基于双序前馈解耦的重复控制和比例积分控制器相结合的控制方法,在电网电压处于非理想状态时,虽然在一定程度上相比于单独的PI控制器能够减小并网电流的谐波含量,但是当电网电压中含有低次谐波分量时,该方法并不能有效地降低由此引起的并网电流中的低次谐波含量,文献[16 ]提出利用比例积分谐振控制器来消除由网侧电压畸变引起的单相变流器交流电流中的低次谐波,但是该文献中对于参数整定的过程较为模糊且无法得出控制器参数具体的选择范围,没有明确的约束规则,使得系统无法工作在较为理想的状态.文献[17 ⇓ -19 ]提出一种有限集模型预测控制,实现电网不平衡下并网控制,该方法不需要复杂的调制策略,但是为了满足并网要求,需要较大的总谐波失真(Total harmonic distortion,THD),因此会增加系统成本.文献[20 ]针对低次谐波抑制问题,提出基于自适应陷波器的谐波抑制方法.通过在主电流环中加入基于自适应陷波器的谐波抑制策略,可同时抑制多次谐波电流,具有控制结构简单的优点,取得了较好的效果.但其采用的自适应算法较复杂,其中步长参数选择会对算法收敛性影响较大从而影响谐波补偿效果. ...
1
2014
... 随着越来越多的新能源接入电网,电网电压中处于不平衡以及含有谐波等非理想状态是不可避免的,当电网电压处于非理想状态时,受到电网电压负序和谐波分量的影响,传统控制策略下的并网逆变器输出电流将会发生畸变,低次谐波含量高以及产生输出功率波动等问题,使逆变器和电网的运行情况恶化.为了解决电网电压处于非理想状态时传统控制策略下的并网逆变器所出现的问题,文献[9 ⇓ ⇓ ⇓ -13 ]提出的控制策略在dq 坐标系下采用比例积分(Proportional integral,PI)控制器和αβ 坐标系下采用比例谐振(Proportional resonance,PR)控制器来对并网电流进行控制.但是,当电网电压不可避免地会发生畸变导致电网电压中含有低次谐波分量时,采用比例积分控制方法会导致并网电流含有相应的谐波分量,进而导致并网电流含有较大的低次谐波分量;采用比例谐振控制方法虽然能够有效地抑制并网电流中的低次谐波分量,但是当电网处 于不平衡时会导致输出电流不平衡.文献[14 -15 ]提出基于双序前馈解耦的重复控制和比例积分控制器相结合的控制方法,在电网电压处于非理想状态时,虽然在一定程度上相比于单独的PI控制器能够减小并网电流的谐波含量,但是当电网电压中含有低次谐波分量时,该方法并不能有效地降低由此引起的并网电流中的低次谐波含量,文献[16 ]提出利用比例积分谐振控制器来消除由网侧电压畸变引起的单相变流器交流电流中的低次谐波,但是该文献中对于参数整定的过程较为模糊且无法得出控制器参数具体的选择范围,没有明确的约束规则,使得系统无法工作在较为理想的状态.文献[17 ⇓ -19 ]提出一种有限集模型预测控制,实现电网不平衡下并网控制,该方法不需要复杂的调制策略,但是为了满足并网要求,需要较大的总谐波失真(Total harmonic distortion,THD),因此会增加系统成本.文献[20 ]针对低次谐波抑制问题,提出基于自适应陷波器的谐波抑制方法.通过在主电流环中加入基于自适应陷波器的谐波抑制策略,可同时抑制多次谐波电流,具有控制结构简单的优点,取得了较好的效果.但其采用的自适应算法较复杂,其中步长参数选择会对算法收敛性影响较大从而影响谐波补偿效果. ...
电网不平衡时抑制有功功率二次波动的并网逆变器控制策略
1
2014
... 当非理想电网情况出现时,若仍采用理想电网下的控制结构,网侧电流中的负序分量将会无法得到控制,从而引起逆变器交流侧过电流,电流谐波增大的情况,这些问题轻则影响并网逆变器的正常运行,重则烧毁器件[21 ] ,为了解决这一问题,需要对网侧电流中的正序、负序分量分别进行控制. ...
Grid-connected inverter control strategy for restraining the secondary fluctuation of active power when the grid is unbalanced
1
2014
... 当非理想电网情况出现时,若仍采用理想电网下的控制结构,网侧电流中的负序分量将会无法得到控制,从而引起逆变器交流侧过电流,电流谐波增大的情况,这些问题轻则影响并网逆变器的正常运行,重则烧毁器件[21 ] ,为了解决这一问题,需要对网侧电流中的正序、负序分量分别进行控制. ...
Optimized design of stationary frame three phase AC current regulators
1
2009
... 由图10 可知,此时系统的截止频率fc 为1 416 Hz,根据文献[22 -23 ]中的经验公式可知Kr 的取值可由式(22)得到 ...
Harmonic suppression and stability enhancement for parallel multiple grid-connected inverters based on passive inverter output impedance
1
2017
... 由图10 可知,此时系统的截止频率fc 为1 416 Hz,根据文献[22 -23 ]中的经验公式可知Kr 的取值可由式(22)得到 ...